计数资料统计推断
（一）样本率的抽样分布与抽样误差
与前面描述样本均数的情形类似，由于个体差异的存在，在随机抽样的过程中同样会产生样本频率与样本频率之间、样本频率与总体概率之间的差异，也称率的抽样误差。
根据二项分布原理，若随机变量X～B（n，π），则样本频率p=x 
n
的总体概率为π，标准误为
率的标准误越小，用样本频率估计总体概率的可靠性越好；反之，用样本频率估计总体概率的可靠性越差。同时，频率的标准误与样本含量n的平方根成反比，增加样本含量可以减少样本频率的抽样误差。
在实际工作中，总体概率π一般是未知的，常用样本频率p来近似地代替，得到标准误的估计值
【例9.20】抽样调查某大学大二男生1000人，其中近视眼患者637人，患病率为63.7%，试估计在此次抽样中所产生的抽样误差。
【解】已知样本率p=63.7%，样本量n=1000，直接代入公式（9.28），率的标准误为
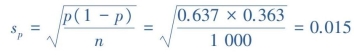
（二）总体概率的区间估计
对于二分类定性变量资料，其总体概率的区间估计及其目的、含义和注意事项与总体均数的区间估计完全一致，不再赘述。具体的总体概率π的（1-α）置信区间估计方法可根据样本含量n和样本频率p的大小而做出选择。
1.查表法
对于小样本资料，如n≤50，特别是当p非常接近0或1时，可通过查百分率的置信区间表（附表3）来直接确定总体概率π的95%或99%置信区间。
【例9.21】某校医对某地36名大二女生进行眼科检查，发现沙眼患者3人。试估计该地大学所有大二女生沙眼患病率的95%置信区间。
【解】由附表3可查得，在n=36与x=3交叉处的上行数值（95%置信区间）为2～22，即该大学所有大二女生沙眼患病率的95%置信区间为2%～22%。
附表4中仅列出了x≤n/2的部分，当x＞n/2时，应以n-x代替x查附表3，再用100减去查得的数值，即为所求的置信区间。
【例9.22】在例9.21中，若该校医在36名大二女生中发现了有25例近视眼患者。试估计该大学所有大二女生近视眼患病率的95%置信区间。
【解】本例中，n=36，x=25＞36/2，故用n-x=11代替x；查附表4，为16～48；再用100减去查得的数值，得到该大学所有大二女生近视眼患病率的95%置信区间为52%～84%。
2.正态近似法
当二项分布的n足够大且np及n（1-p）同时≥5时，p的抽样分布近似正态分布，总体概率π的双侧（1-α）置信区间近似地等于：
【例9.23】抽样调查某地大二男生1000人，其中近视眼患者637人，患病率为63.7%。试估计该地大二男生近视眼总体患病率的95%置信区间。
【解】本例中，n比较大，且np=637及n（1-p）=363，均大于5，可近似地估计总体概率的双侧95%置信区间：
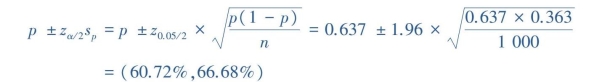
即该地大学大二男生近视眼总体患病率的95%置信区间为（60.72%，66.68%）。
（三）χ2检验
χ2检验（Chi-square Test）是英国统计学家Karl Pearson提出的一种主要用于分析计数资料的假设检验方法。该方法的主要目的是推断两个或多个总体率或构成比之间有无差别。
1.χ2检验基本思想
【例9.24】为探讨温针灸在退行性膝关节炎治疗中的临床应用价值，将80例退行性膝关节炎患者随机分为两组，分别给予西医治疗及温针灸治疗，比较两组患者的疗效。结果见表9.13。试问：两种治疗方法的有效率是否不同？
表9.13 两种疗法治疗退行性膝关节炎的疗效
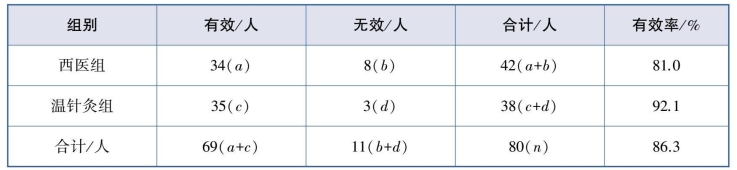
【解】本例中，“疗效”是二分类的定性资料。表9.13中，基本数据由2行、2列构成，即34（a）、8（b）、35（c）、3（d）是4个最基本的数据，其余数据可以由这4个基本数据计算出来，这种资料被称为四格表（Fourfold Table）或2×2表。该案例的分析目的是要通过比较两个样本率，来推断两种疗法的总体有效率有无差异。
假设两个总体有效率相等（π1=π2），可以用合计有效率（86.3%）作为两总体有效率的估计值。按此估计值，理论上中医组有效人数应为42×86.3%=36.2（人），无效人数为42×（1-86.3%）=5.8（人）；温针灸组有效人数为38×86.3%=32.8（人），无效人数为38×（1-86.3%）=5.2（人）。
若两个总体有效率相等的假设成立，实际频数和理论频数的吻合度应该较高。其吻合度以假设检验统计量χ2度量。
χ2服从自由度ν=（R-1）（C-1）的χ2分布，其中R为行数，C为列数。
式中，A是实际频数（Actual Frequency），T是理论频数（Theoretical Frequency）。表9.13中，a、b、c、d所对应的理论频数T分别为36.2，5.8，32.8，5.2。可见，第R行C列对应格子的理论频数TRC计算公式为
式中，nR为相应的行合计；nC为相应的列合计；n为总例数。
可以看出，χ2检验的基本思想是检验实际频数和理论频数的差别是否由抽样误差所引起。χ2值的大小反映了实际频数与理论频数的吻合程度。在H0（H0∶π1=π2）成立的条件下，实际频数与理论频数相差不应该很大，即χ2值不应该很大。若得到的χ2值很大，说明实际频数与理论频数的差距大；当χ2值超过了设定的检验水准所对应的χ2界值（如χ2≥χ02.05），则P≤0.05，说明实际频数与理论频数的差别由抽样误差引起的可能性很小，有理由拒绝H0，接受H1（如H1∶π1≠π2）。若得到的χ2值不是很大（如χ2＜χ02.05），则P＞0.05，说明实际频数与理论频数的差别由抽样误差引起的可能性很大，此时则不拒绝H0。
2.四格表资料的χ2检验
对于完全随机设计两个率比较的资料，可整理为形式如表9.13的四格表，因而完全随机设计两个率比较的χ2检验又称为四格表资料的χ2检验。
1）四格表资料χ2检验的基本步骤
以例9.24为例，说明四格表资料χ2检验的基本步骤。
（1）建立检验假设，确定检验水准
H0∶π1=π2，即两种疗法的有效率相同；H1∶π1≠π2，即两种疗法的有效率不同；α=0.05。
（2）计算检验统计量
根据公式（9.31）计算理论频数：
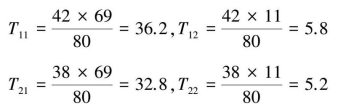
根据公式计算χ2值：
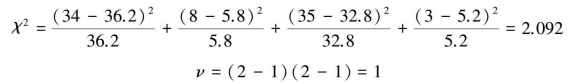
（3）确定P值，作出统计推断
查附表4，得χ02.1，1=2.71，χ02.25，1=1.32，0.1＜P＜0.25，按α=0.05检验水准，不拒绝H0，尚不能认为两种疗法的有效率不同。
对于四格表资料，也可采用下式计算χ2值。该式被称为4个表资料χ2检验专用公式。
例9.24的计算结果如下，与基本公式完全等价。
由于χ2分布是一种连续性分布，当应用于样本含量较小的定性变量资料比较时，计算出来的χ2值往往偏大，相应的P值偏小，从而人为地增加了犯第Ⅰ类错误的机会。为纠正这种偏性，美国统计学家F.Yates提出了χ2的连续性校正法（Correction for Continuity），校正公式为
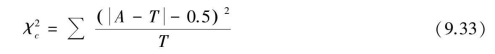
或
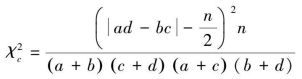
2）四格表资料χ2检验的注意事项
对于四格表资料，采用χ2检验时，应注意以下问题：
①当n≥40，且所有格子的T≥5时，用四格表χ2检验的基本公式或专用公式计算χ2值。
②当n≥40，但有1≤T＜5的格子时，用校正公式计算χ2值为宜。
③当n＜40或T＜1时，不宜计算χ2值，需采用四格表确切概率法直接计算概率。
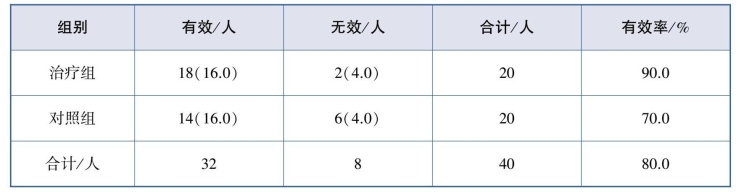
【例9.25】观察达芬霖喷雾剂治疗小儿急、慢性鼻炎的临床疗效。将40例小儿急、慢性鼻炎患者随机分为治疗组和对照组，治疗组20例用达芬霖喷雾剂，对照组20例用麻黄素滴鼻剂，治疗组与对照组治疗小儿急、慢鼻炎总有效率分别为90.0%、70.0%，数据见表9.14。试问：两种治疗方法的有效率是否不同？
表9.14 两种疗法治疗小儿急、慢性鼻炎的临床疗效
【解】假设检验步骤：
（1）建立检验假设，确定检验水准
H0∶π1=π2，即两种疗法的有效率相同；H1∶π1≠π2，即两种疗法的有效率不同；α=0.05。
（2）计算检验统计量
计算每个格子的理论频数，标在表9.14括号内。本例中，n=40，但有两个格子的理论频数为4，需要使用四格表χ2检验的校正公式。
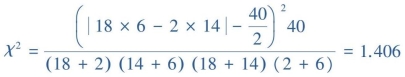
（3）确定P值，作出统计推断
查附表4，得χ02.1，1=2.71，χ02.25，1=1.32，0.1＜P＜0.25，按α=0.05检验水准，不拒绝H0，尚不能认为两种疗法的有效率不同。
3.配对四格表资料的χ2检验
对于配对设计两个率比较的资料，可整理为形式如表9.15所示的四格表，因而配对设计两个率比较的χ2检验又称为配对四格表资料的χ2检验。
【例9.26】分别采用巢式PCR（A法）和β-D-1，3-葡聚糖试验（B法）检测104例临床胸腹水标本中真菌，结果见表9.15。试比较两种方法的阳性率有无差异？
表9.15 两种方法的检测结果
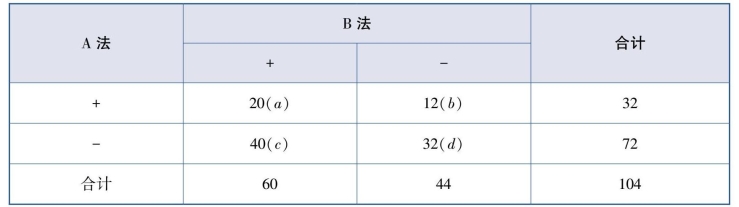
【分析】本例中，同一份标本分别用两种不同方法检测，“检测结果”为阳性或阴性。因此，该资料是配对设计的二分类定性变量资料。两种方法对一份标本的检测结果有4种情况：A+且B+为a，A+而B-为b，A-而B+为c，A-且B-为d。由于A、B两法一致阳性数a和一致阴性数d是两法检测相同的结果，如果要比较A、B两法的阳性率有无差异，a、d不提供差异信息，只要比较b和c即可，采用配对差异性χ2检验（或称McNemar检验）。其检验统计量为
若b+c＜40，校正公式为
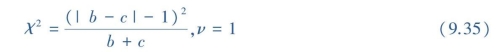
【解】假设检验步骤如下：
（1）建立检验假设，确定检验水准
H0：两种方法测定的阳性率相同，即总体B=C；H1：两种方法测定的阳性率不同，即总体B≠C；α=0.05。
（2）计算检验统计量
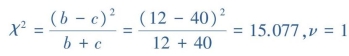
（3）确定P值，作出统计推断
查附表4，得χ02.005，1=7.88，P＜0.005，按α=0.05检验水准，拒绝H0，接受H1，差异有统计学意义，可认为A、B两种方法的测定结果有差别，B法测定阳性率较高。
4.行×列表资料的χ2检验
1）行×列表资料的χ2检验方法
对于完全随机设计多个组率的比较或两个（多个）组构成比较的资料，可整理为R行C列的行×列表，相应χ2检验也称为行×列表资料的χ2检验。
【例9.27】调查新疆不同民族青年人恒牙先天缺失疾病的现况，结果见表9.16。试分析不同民族青年人恒牙先天缺失患病率有无不同？
表9.16 不同民族间恒牙先天缺失患病率的比较
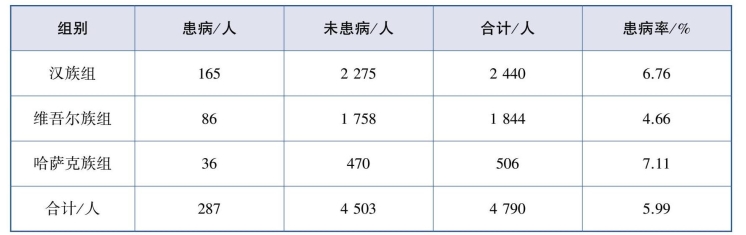
【分析】本例中，数据资料是完全随机设计的3组二分类定性变量资料的比较，目的是比较3个民族的患病率是否不同，可考虑采用行×列表资料的χ2检验。行×列表资料的χ2检验可使用χ2检验的基本公式，也可使用基本公式的展开式。
【解】假设检验步骤如下：
（1）建立检验假设，确定检验水准
H0∶π1=π2=π3，即3个民族的患病率相同；H1∶π1、π2、π3不全相等，即3个民族的患病率不全相同；α=0.05。
（2）计算检验统计量
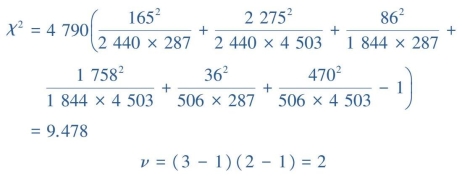
（3）确定P值，作出统计推断
查附表4，得χ02.010，2=9.21，χ02.005，2=10.60，0.005＜P＜0.010，按α=0.05检验水准，拒绝H0，接受H1，差异有统计学意义，可认为3个民族患病率不全相同，但尚不能认为任意两个民族之间都不同。如果要了解每两个民族之间患病率是否不同，需要进一步做率的两两比较。
2）多个样本率间的多重比较
样本率多重比较的方法有很多种，常见方法有Bonferroni、Scheffe法等。这里只介绍最简单的Bonferroni法，其基本思想是根据两两比较的次数重新确定检验水准α′。该方法比较保守，比较的组数不宜过多。重新确定检验水准α′的方法通常有两种情况：
①多个实验组间的两两比较：α′=Cαk2=2α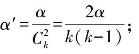
k（k-1）；
②多个实验组与同一对照组的比较：α′=α
k-1，式中，k为参加比较的组数。
对例9.27进一步进行率的两两比较，以推断任意两个民族的患病率有无不同。本例为3个样本率的两两比较，调整检验水准为
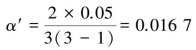
采用四格表的χ2检验对任两个民族患病率进行比较，结果见表9.17。按α′=0.0167检验水准，汉族与维吾尔族的患病率差异有统计学意义，汉族与哈萨克族、维吾尔族与哈萨克族的患病率差异均无统计学意义。
表9.17 3个民族间患病率的两两比较
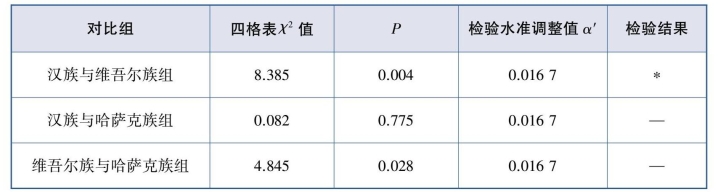
注：表中“*”表示差异有统计学意义，“—”表示差异无统计学意义。
3）行×列表χ2检验的注意事项
①行×列表χ2检验的条件是理论频数不宜太小，一般规定：不能有理论频数小于1的格子，理论频数1≤T＜5的格子数不超过总格子数的1/5。如果有1/5以上格子的理论频数1≤T＜5，可采用以下处理办法：
a.增加样本含量，以增大理论频数。
b.将理论频数太小的行或列与性质相近的邻行或邻列中的实际频数合并。合并后可以产生较大的理论频数，但要注意相邻类别合并要符合专业知识，合并后要有实际意义。
c.删去理论频数太小的格子所在的行或列。
最好采用“增加样本含量”的方法，后两种方法将会丢失部分信息，也可能破坏样本的随机性。因此，研究设计时应考虑足够的样本含量。
d.从统计方法学角度，可采用Fisher确切概率法检验。
②进行多个样本率比较的χ2检验，拒绝H0时，只能认为各总体率不全相同（至少有两个总体率不相同），而不能认为每两组之间都有差异。如果需要知道各组之间是否有差异，需要进一步进行两两比较。
③在实际应用中，要根据行×列表资料的类型和研究目的选用恰当的分析方法。χ2检验适用于“效应”为无序分类指标的行×列表资料。当“效应”为有序指标的行×列表即等级资料时，若了解不同组别“效应”总体构成比有无不同，仍然可考虑采用χ2检验；若了解不同组别“效应”总体水平有无不同，一般用秩和检验分析更适宜。
※思考题
1.总体均数的置信区间与医学参考值范围有何区别？
2.按α=0.10检验水准做t检验，P＞0.10，不能认为两总体均数不相等。此时，若推断有错，则犯了假设检验第几类错误？犯错概率是多少？
3.分别用两种方法检查已确诊的乳腺癌患者120名。甲法的检出率为60%，乙法检出率为50%，甲乙两法阳性一致的检出率为35%，哪种方法的总体检出率高？
（雷迅）