二、正态分布
正态分布是计量资料最常见的一种分布类型。生物医学中很多指标的测量值,如身高、体重、血红蛋白、甘油三酯等近似服从正态分布。同时,一些重要的分布(如t分布)以正态分布为基础而导出。正态分布还是其他一些分布(如二项分布)的极限分布形式。应该说,正态分布是医学统计学中最重要的分布类型。
(一)正态分布
正态分布(Normal Distribution)呈现为一条单峰对称的钟形曲线,其曲线两端永远不与横轴相交。其概率密度函数为

式中,两个常数分别为π(圆周率)与e(自然常数);两个参数分别为μ与σ2,μ为反映集中位置的总体均数,σ2为反映离散程度的总体方差。习惯上将随机变量X服从于均数为μ、方差为σ2的正态分布记作X~N(μ,σ2)。
具体地,正态分布具有以下几个特点:
①单峰对称的“钟形”曲线。
②X可取任意实数。
③μ决定正态分布曲线的峰在横轴上的位置[图9.3(a)]。当σ2恒定时,μ越大,曲线将向右平移;反之,曲线则向左平移。
④σ2决定正态分布曲线的形状[图9.3(b)]。当μ恒定时,σ2越大,曲线越“矮胖”;反之,曲线则越“高瘦”。

图9.3 正态曲线位置、形状与μ、σ2关系示意图
⑤正态曲线下的面积分布有一定规律。曲线下面积即为概率,总面积为1(概率为100%)。由正态曲线累积分布函数可知,代入横轴取值可得相应左侧尾端面积,继而可求得横轴上一些特殊界点与曲线下的面积关系,见图9.4。
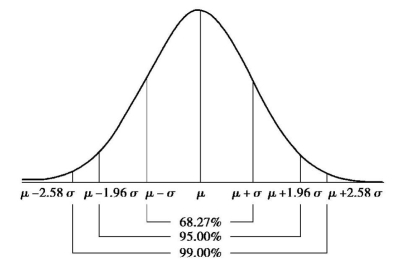
图9.4 正态曲线下面积与横轴界点对应关系
(二)标准正态分布与z变换
不同的均数和方差将决定正态分布的位置和形态。因此,统计学家提出对任意一个服从正态分布N(μ,σ2)的随机变量,均可作如下的标准化变换,也称z变换(或u变换)。
![]()
经此变换得到的变量z的概率密度函数为
![]()
变换后的z值仍然服从正态分布,且其总体均数为0、总体方差为1。我们称此正态分布为标准正态分布(Standard Normal Distribution),用z~N(0,12)表示(图9.5)。
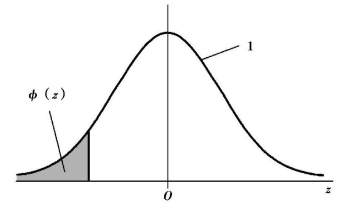
图9.5 标准正态分布的分布函数示意图
由于其位置和形态均被固定,标准正态分布曲线是唯一的一条曲线,其曲线下面积规律如下:
①曲线下横轴上的面积之和为1,即概率之和为100%;
②任意两点间的面积可由积分实现,而且统计学家已编制标准正态分布曲线下左侧尾部面积表(附表1)供读者查阅。附表1内所列数据表示z取不同值时z值左侧标准正态曲线下面积,记作φ(z)。而右侧的曲线下面积则可通过正态分布曲线的对称性获得。值得一提的是,任意一条正态分布曲线下的面积分布规律均可通过z变换公式转化后,与标准正态分布曲线下的面积相对应。
具体地,附表1中横标目与纵标目的数值都是标准正态分布曲线下横轴上的z值。横标目为z值的整数和第1位小数,纵标目为z值的第2位小数。它们交叉位点上的数值就是该z值所对应的标准正态分布的左侧尾部面积。
【例9.9】已知X服从均数为μ、方差为σ2的正态分布,请估计X取值在区间μ±1.96σ内的概率。
【解】欲求X取值在相应区间内的概率,实则求其在该区间的曲线下面积,需首先获得区间两端点所对应的标准正态分布曲线上z值。
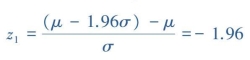
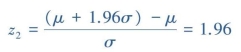
查附表1,φ(-1.96)=0.025。由对称性可得,区间(+1.96,+∞)上的曲线下面积也是0.025,故z值取值于(-1.96,+1.96)的概率为1-2×0.025=0.95,即X取值在区间μ±1.96σ内的概率为95%。
【例9.10】已知某地健康成年男子的血清总胆固醇测量值近似服从正态分布,其μ=4.95mmol/L,σ=0.85mmol/L。试估计该地健康成年男子的血清总胆固醇测量值在6mmol/L以上者占该地男子总数的百分比。
【解】计算6mmol/L对应的z值,可得
![]()
查附表1,寻找标准正态曲线下z=1.24的右侧面积,即该地健康成年男子的血清总胆固醇测量值在6mmol/L以上者占该地男子总数的百分比。因为正态分布的对称性,可查到φ(-1.24)=0.1075,即该地健康成年男子的血清总胆固醇测量值在6mmol/L以上者占该地男子总数的10.75%。
