风险判断偏差对投保决策的影响
将上述风险判断偏差规律与上一节的研究结论相结合，得到如下群体投保规律：
第一，人们不是高估风险，就是低估风险，因此，几乎所有人的保险需求强度都偏离理性状态。
第二，当客观概率很低时，低估概率者占比很大且低估倍数很大，高估概率者占比很小且高估倍数很大，导致保险需求呈两极分化特征。即，当客观概率很低时，多数人低估风险且低估倍数很大将导致多数人的保险需求强度远低于理性状态，基本处于放弃投保的状态；少数人会高估风险且高估倍数很大将导致少数人的保险需求强度远高于理性状态，处于急于购买保险的状态。出险概率越低，上述两极分化特征越突出。
第三，随着客观出险概率的增加，高估风险者占比迅速增加，低估风险者占比迅速降低，高估倍数和低估倍数迅速降低。从第四节分析来看，这意味着，在本章第三节的假设条件下，当客观概率大致在0.03左右时，高估风险者占比就会超过50%，导致多数人的保险需求强度高于理性状态。
第四，客观概率继续增加，在0.05～0.1之间某处时，高估概率者占比开始掉头下降，低估概率者占比开始掉头上升，双方都向50%逼近。这意味着，从客观概率等于0.05～0.1之间某处开始，趋势大变，保险需求强度高于理性状态的人占比开始减少，保险需求强度低于理性状态的人占比开始增加，双方占比都在向50%逼近。
第五，随着客观出险概率增加，高估风险人群的高估倍数都越来越小，导致高估概率者的需求强度逐渐下降；低估风险人群的低估倍数越来越小，导致低估概率者不想买保险的程度也逐渐下降；双方都趋于理性。
第六，尽管存在风险判断偏差，但人们坚信自己的判断是正确的，这意味着，尽管人们的保险消费呈现如上非理性特征，但人们却以极大的信心坚持自己的决策是正确的。
【注释】
[1]大脑在整个身体中的能量消耗是相当大的，重量占比约5%的大脑消耗了整个身体约20%的能量，从负荷和节约能量来看，大脑的运行也追求成本与收益的平衡，所以，大脑并不会对每件事都进行深入的思考和计算。
[2]“启发式”这个术语来自数学和计算机科学，这两个学科区分了算法和启发式，算法是指解题方案的准确而完整的描述，代表着用系统的方法描述解决问题的策略机制，通常效率较低；而启发式是指用一种更有效率的方法解决同样的问题，但通常会得到有偏的结果。
[3]可能是受到奈特的影响，很多书籍和论文将保险风险、赌场风险、彩票风险视为风险而非不确定性，其实是混淆了主体的区别。对于保险公司来说，保险风险是风险，但对于保险客户而言，保险风险其实属于不确定性。同样，赌场风险对于赌场老板来说是风险，但对赌徒是不确定性；彩票风险对博彩公司是风险，对买彩票者是不确定性。
[4]想想我们早上刚到办公室，其实有许多正事要办。但是，摊开文件或打开电脑后，我们的视线却不由自主地移动到了手机上，打开微信或其他App一路看了下去，感觉时间过得飞快，这就是系统1在起作用；只有当某件正事的最后期限逼近时，我们才被逼无奈地开始硬着头皮开始工作，感觉时间也变慢了，这是系统2在起作用，中间还时不时地受到系统1的影响，不自觉地去看看手机微信。
[5]塔勒布在《黑天鹅》中非常形象地说：“人生就像驾车，驾驶员是情感（系统1），理智（系统2）通常在副驾驶睡觉。”
[6]在不确定状况下的判断的研究中，学者们普遍采用的研究范式是，将被试的判断结果和规范模型的结果进行比较，进而检验是否存在判断偏差以及偏差大小。
[7]下面的分析思路其实是“事后诸葛亮”，是我根据后面的分析过程“事后”总结形成的，读者看起来会有些吃力。建议读者先囫囵吞枣看过去，等读完后再返回来看分析思路时，就容易理解了。
[8]主观概率超过了1，有些不合常理。不过，从后续分析可以看出，对于客观概率p≤0.2的保险风险来说，主观概率超过1的可能性几乎为零。
[9]这里的思维方式，是二项分布的泊松逼近，即当n≥20、p≤0.05时，用泊松分布作为二项分布的近视值，计算效果颇佳。不过，同事朱少杰博士认为，可直接使用《非寿险精算》中的“同质保单组合的索赔次数模型”进行计算，该模型认为在保单同质和相互独立的条件下，保单组合中随机抽取的一份保单在一年内发生k次索赔的概率服从泊松分布，这样，就不必将1年拆分为4个季度了。从计算过程来看，无论是否将1年拆分成四个季度，计算结果都是相同的。最后要声明的是，采用泊松分布的计算结果，仍然是一种近似计算，结果并不精确，但用于分析风险判断偏差的变化规律，应该是足够了。关于“同质保单组合的索赔次数模型”，读者可参看：李恒琦，非寿险精算，西南财经大学出版社，2004，第86—95页。
[10]也可理解为：人群占比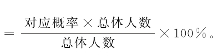
[11]可以预计，当考虑5年以上直接经历时，图5－4中的转折点会随着年数的增加而向左移动，例如，当考虑7年直接经历时，转折点变为“客观概率＝1/7或0.143”；当考虑8年直接经历时，转折点变为“客观概率＝1/8或0.125”。同样可以预计，当考虑5年以下直接经历时，客观概率p≤0.2时，图5－4中的转折点就消失了，高估（低估）风险者占比会随客观概率的增加而持续增加（降低）。但总体来看，图5－4展现的基本规律是稳健的。
[12]在边际效用投保决策模型中，如式（4－8）所示，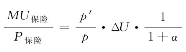
，这意味着，高估倍数＝10，则
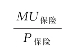扩大10倍，可粗略地理解为投保意愿提升10倍；低估倍数＝10，则
缩小10倍，可粗略理解为投保意愿缩小10倍。
[13]这种影响既是人们的直觉反映，也是理性的表现。风险发生的统计概率，就是依据对大量人群出事频率进行统计的计算结果，其内在的假定是：对于相同种类的风险，每个人都有相同的出险概率。这一假定反映了理性人对他人遭受的风险事件会感同身受。
[14]纳扎波尔蒂•圣捷尔吉•阿尔伯特（1893—1986），因“与生物燃烧过程关的发现，特别是关于维生素C和延胡索酸的催化作用”而获得了1937年的诺贝尔生理学有或医学奖。
[15]心理学研究表明，当损失场景栩栩如生时，人们会产生强烈的情感反应，此时人们对损失后果非常恐惧；反之，当只是听到某某风险事故，但缺乏栩栩如生的场景时，就很难引发人们的情感反应，对人们的风险判断影响较低；当风险距离很大时，人们甚至不知道风险事故的发生，处于忽略风险的状态。
[16]读者在文中会看到“高估倍数”和“平均高估倍数”，两者意思相同；还会看到“低估倍数”和“平均低估倍数”，两者意思也相同。之所以这样写，是为了表达意思方便。
[17]我猜测，高估倍数曲线与低估倍数曲线是不完全上下对称的。原因是，我认为，低估风险和高估风险可能存在某种总体平衡关系，当出险概率很低时，低估概率者占比远高于高估概率者占比，意味着前者的低估程度应该低于后者的高估程度。
[18]泰坦尼克号超级游轮于1912年4月处女航时撞上冰山后沉没。泰坦尼克号船长史密斯在泰坦尼克号建造期间曾说：“根据我所有的经验，我没有遇到任何值得一提的事故。我在整个海上生涯中只见过一次遇险的船只。我从未见过失事船只，从未处于失事的危险中，也从未陷入任何有可能演化为灾难的险境。”也许，正是船长的高度自信酿成了大祸。
[19]结合问题14′，卡尼曼和特沃斯基解释了人们为何愿意为小概率损失风险购买保险，他们认为，人们选择D类似于愿意为风险C购买保险。具体解释是，前景理论中，损失部分的价值函数反映出人们对损失风险表现出风险喜好，但决策权重函数中人们对小概率事件的过度重视反映出人们可能愿意出高价购买保险，最终，当人们对小概率事件的过分看重压过风险喜好时，人们会选择为小概率风险购买保险。
[20]读者可以想象，随着保额增加，ΔU会越来越逼近ΔU′，只有当
时，个体才会购买足额保险，并最终达到ΔU＝ΔU′。因此，在附加费率为零的条件下，低估风险必然会使
，个体只能购买部分保险。
[21]如果风险低估程度严重到刚出手购买保险（如花1元钱购买保险、或仅购买1元保额）就出现
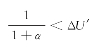的现象（此时ΔU取其最大值ΔUmax），个体就会彻底放弃购买保险。
[22]不得不说，互联网和人工智能技术已经可以大幅降低交易成本，进而将不少保单的保额降到很低的程度。如网购退货运费险，保额可能只有几元钱。但不是所有渠道所有保单都可以承受极低的保额。