贴现效用模型的形式

贴现效用模型描述在多时期情形下，个体如何对未来多期消费束（c0，c1，…，cT）进行选择。在偏好满足完备性和传递性的前提下，处于时期0的个体面临的跨期总效用函数可表达为U0（c0，c1，…，ct），并假设：一是效用可以实施基数计量，二是个体的跨期总效用可拆分为由各期“子效用”贴现加总的形式，三是每期效用均在期末而非期间获取，由此，萨缪尔森将跨期总效用表达为：

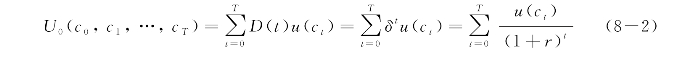
其中，

c0，c1，…，cT表示从时期0到时期T的消费计划；

U0（c0，c1，…，ct）表示从时期0到时期T的消费计划c0，c1，…，cT在当下或时期0的总效用；

u（ct）表示个体在时期t消费ct所获得的瞬时效用；

D（t）＝δt是个人的贴现函数，表示在时期0时，个体对时期t获得的效用所赋予的权重，或者说，时期0，1，2，…，T的效用将分别以1，δ，δ2，…，δT的比例折现；

r表示个体对未来效用的贴现率，也称时间偏好率，在萨缪尔森的模型中，r是逐期固定不变的；

δ＝1/（1＋r）是每期贴现因子，用每期贴现因子乘以时期t＋1的效用就可以得到这些效用贴现到时期t的值。

有了这个总效用计算公式，就可以据此计算不同选择方案的跨期总效用，进而选择总效用最大的方案，这就将多时期的跨期选择行为用标准经济学模型，即效用最大化模型进行了描述。