象和数学映射

笛卡儿通过建立空间坐标，将数学中的自变量和因变量之间的对应关系以图像描述，使空间坐标之间形成象与原象之间的映射关系，并划分了象限。其实数学上的映射关系与中国古代事物之间取象比应原理相似。通常情况下，映射一词有照射的含义，又称映照。在数学上，映射是个术语，指两个集合之间元素的相互“对应”的关系，是比函数更广泛的数学概念，通过映射观念，可以揭示事物之间看似不相关的联系。数学上的映射是两个集合中的一种特殊的对应关系，即如果按照某种对应法则，对于集合A中的任何一个元素，在集合B中都有特定的元素与它对应，那么这样的对应（包括对应法则）称为集合A到集合B的映射。映射是互逆的，也就是每个象总有自己的原象，每个原象也对应自己的象。例如，设A和B是两个非空集合，f是一个法则，如果对A中任一元素x，依照法则f，B中都有某一元素y与x相对应，就称f为一个从A到B的映射。常记作f ：A→B，表示从A到B的映射，A称为映射的定义域；反之，f -1：B→A，表示从B到A的逆映射（图6-25）。数学上的映射有严密的运算关系，为了表示元素x的对应元素y，常写为y=f （x），并称y为x在映射f之下的象，x为原象。f为映射法则，是连接A（y）和B（x）的纽带，也就是A（y）和B（x）的关联性。在现实生活中，有许多映射没有严密的运算关系，但却有性质上的对应关系，而且对应关系很复杂，可以一对一、一对多、少对多，或是多对一、多对少等（图6-26）。艺术创作或创意设计可以看作是象和原象之间的多级复杂映射关系，对象和原象的映射关系解析或许是揭示艺术创作或创意设计规律的有效途径。

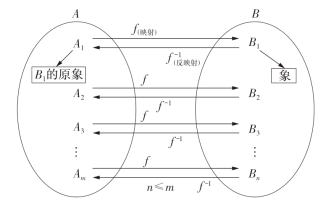
图6-25　数学上的映射关系

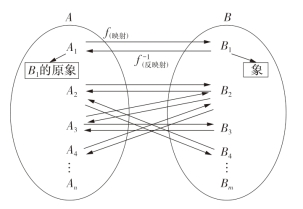
图6-26　意象设计中的复杂映射关系