五 教学过程
(一)复习旧知,唤醒导入
1.教师陈述。我们在学习《概率的进一步认识》这一章前已经学过《概率初步》一章,接下来我们先通过4个题目来回顾已经学过的相关知识。大屏幕依次呈现4个题目。
——问题1:随机事件的概念
下列事件中,哪些是必然事件?哪些是不可能事件?哪些是随机事件?
A.抛出的篮球会下落;
B.一个射击运动员每次射击的命中环数;
C.任意买一张电影票,座位号是2的倍数;
D.早上的太阳从西方升起。
——问题2:抛掷一枚硬币
小明和小颖都想去看周末电影,但只有一张电影票。两人决定一起做游戏,谁获胜谁就去看电影。游戏规则如下:抛掷一枚均匀的硬币,如果正面朝上,则小明获胜;如果反面朝上,则小颖获胜,你认为这个游戏公平吗?(硬币直立的情况忽略)
——问题3:用频率估计概率
观察下面的表格,你发现了什么规律?
_____________
历史上的掷硬币实验
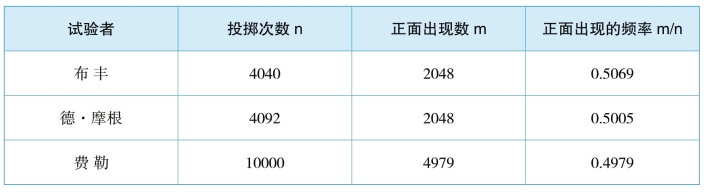
——问题4:直击中考(2019年深圳中考第14题)
现有8张同样的卡片,分别标有数字:1,1,2,2,2,3,4,5,将这些卡片放在一个不透明的盒子里,搅匀后从中随机抽取一张,抽到标有数字2的卡片的概率是________。
2.学生回答。学生独立思考后回答。
3.互动交流。基于上面的4个问题,教师提出几个与概率的基本思想相关的问题并和同学们一起交流。
频率如何计算?
概率与频率的区别和联系?
抛掷一枚硬币,不用试验,我也可以很快算出它正面朝上的概率,这样求概率的类型还有吗?
4.引入主题。“摸球、掷骰子和抽扑克牌。”同学们说了几个古典概型中很常见的事件,他们的结果共同具有有限性和等可能性这两个特点。古典概型可以通过公式计算得出概率,而像抛掷图钉这样的概型,我们就要通过大量试验来计算它发生的概率。接下来,我们再来解决一个新问题。
课堂观察
这4个题目都是七年级学过的知识,对学生来说比较容易,学生答题的速度很快,尤其是第4个中考问题,那么简单,增强了学生学习本章的信心。
(二)预习反馈,因学定教
1.教师展示学生的预习情况。教师展示部分学生的试验报告,整理学生在课前试验中反馈的问题,并在大屏幕上展示。
问题一:抛30次硬币,试验次数不够多,能用来估算概率吗?
问题二:有没有公式可以计算这个事件的概率?必须做试验吗?
2.学生观察同伴的试验结果。学生注意观察老师展出的试验结果,对比感受随机事件的不稳定性。
课堂观察
学生很认真地观察,对同学的试验结果很感兴趣。问题被老师引用的学生很兴奋,同时也有几个学生想开口解答同学提出的问题。
(三)新课讲授,探索新知
——小组合探
____1.合作探究。6个同学为一个小组,依次记录每位组员的试验数据,填写下表。__

2.展示汇报。各个小组汇总所有组员的数据,并把数据展示在黑板上。
3.讨论交流。回顾自己试验的过程,小组讨论以下4个问题。
抛掷第一枚硬币可能出现哪些结果?它们发生的可能性是否一样?
抛掷第二枚硬币可能出现哪些结果?它们发生的可能性是否一样?
在第一枚硬币正面朝上的情况下,第二枚硬币可能出现哪些结果?它们发生的可能性是否一样?如果第一枚硬币反面朝上呢?
根据上面的数据,请你分别估计“两枚正面朝上”“两枚反面朝上”“一枚正面朝上、一枚反面朝上”这3个事件的概率。由此,你认为这个游戏公平吗?
4.小组展示。
第一小组:抛掷第一枚硬币可能出现两个结果,正面朝上或反面朝上,它们发生的可能性一样。
第三小组:抛掷第二枚硬币也可能出现两个结果,正面朝上或反面朝上,它们发生的可能性一样。
第四小组:不论第一枚硬币出现那种结果,第二枚硬币的结果都是两种,正面朝上或反面朝上,不会受到第一枚的影响。
第二小组:由黑板上面的数据,我们估计“两枚正面朝上”的概率是四分之一,“两枚反面朝上”的概率是四分之一,“一枚正面朝上、一枚反面朝上”的概率是四分之二,也就是二分之一。由此,我们认为这个游戏不公平。显然,“一正一反”获胜的可能性大。
5.教师总结。第一枚和第二枚硬币是相互独立,互不影响的,这一点很重要。接下来我们来看黑板上各个小组的试验结果,并汇总全班的试验数据,我们发现随着试验次数的增加,各个随机事件的频率越来越稳定,比如说两枚硬币都是正面朝上的频率稳定在0.25附近,那我们就可以用频率估计概率,该事件发生的概率就是0.25。
课堂观察
小组长积极地统计组员们的试验数据,同学们讨论积极,小组代表积极发言,组员们认真聆听,对其他小组的试验结果非常关注。
——例题精讲
1.教师引导。回顾一下,我们抛掷一枚硬币时会出现两种结果,正面朝上或反面朝上,它们是等可能出现的,那硬币正面朝上或是反面朝上的概率自然就是二分之一。对于连续抛掷两枚硬币的试验,我们通常借助树状图或表格列出所有可能出现的结果。先来看屏幕上的树状图,如下:
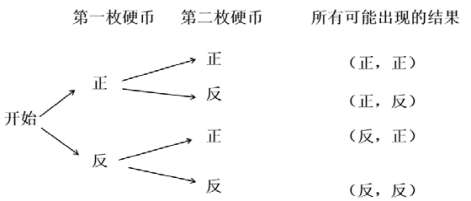
2.教师讲解。开始试验时,第一枚硬币出现两种情况,正或反,接下来抛掷第二枚硬币,不论第一枚硬币出现什么情况,第二枚硬币都不受影响,两枚硬币是相互独立的,还是正或反两种情况,结合起来,共有四种结果,分别是(正,正),(正,反),(反,正),(反,反),且它们是等可能出现的。所以P(两正)=1/4,P(两反)=1/4,而一正一反包含其中的两个结果(正,反)和(反,正),所以p(一正一反)=1/2。
3.提出问题。屏幕上呈现空白表格,请同学们填充表格,列举出所有可能出现的结果。
4.合作探究。小组合作完成表格。

5.教师视导。教师在学生填表的过程中及时视导,了解学生们对表格的理解程度,投影展示学生的答案。
6.教师小结。我们经常借助画树状图或列表格的形式使随机试验的结果不重复,无遗漏地列举出来。
课堂观察
通过教师的讲解,学生基本能够理解树状图的意义,并能填写表格来列举随机出现的结果。
——当堂练习
1.教师布置任务。共3题,学生5分钟内完成。
2.学生独立完成。
3.教师视导辅助。教师在学生完成练习的过程中及时视导,了解学生们对新知识的掌握情况,投影学生的典型问题并纠正和评价。
课堂观察
学生的答题速度慢,原因有3点:首先对文字题目的理解不清晰,其次学生在书写上还存在问题,树状图画得不够均匀,预留答题位置太小,最后是作业没有分层布置,基础弱的学生跟不上。
——课堂小结
互动小结,回顾画树状图和列表格的优点和其用法,并说一说自己的困惑。
课堂观察
学生借助老师的诱导,能很快回顾出相关知识,但在独立解题过程中仍存在问题,比如能理解书中例题给出的树状图,自己却没那么容易画出树状图,在“两步试验的相互独立性”的理解上不够清晰。
(四)限时训练,巩固提升
1.教师布置任务。
2.学生限时作答。
课堂观察
这是本章的第一节课,内容比较简单,学生们学起来还算比较轻松。学生答题准确迅速,学习目标基本达成,但树状图和表格画得不够工整,描述性语言不是很规范。
