五 教学过程
(一)回顾旧知,温故知新
1.问题导入。学生在已有理解基础上,用自己的语言表述勾股定理。老师针对学生的表述,提出修正建议,规范学生的语言表述。
2.学生复述勾股定理后,教师提出问题,勾股定理的公式一定是a2+b2=c2的形式吗?
3.思考回答。学生对公式加上了前提,只有当a、b为直角边,c为斜边时,直角三角形三边关系满足a2+b2=c2。为巩固基础回顾定理,学生独立完成课堂导学案,三分钟时间完成第1题至第3题。
课堂观察
教师问及三边关系时学生回答“勾股弦”,学生回复积极但易忽视对问题的理解,这个习惯也常反映在日常练习。复述勾股定理时,学生先选择用文字进行表述“斜边的平方等于两条直角边的平方的和”。刚开始学生对公式的理解是,只有在直角三角形中三边a、b、c关系才满足a2+b2=c2。后续,才有同学补充“只有a、b为直角边,c为斜边时三边a、b、c关系才满足a2+b2=c2”。
(二)探究证明,思维交融
1.播放视频。视频展示现象:三个底面为正方形、厚度相同的四棱柱中,只有底面较小的两个四棱柱注满有色液体。转动时底面较小的两个四棱柱中的有色液体,恰好注入底面较大的四棱柱中。
视频中实验平面示意图如图1。
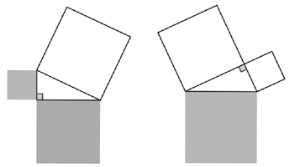
图1
2.探明方向。应用勾股定理为解决直角三角形三边关系提供了简洁的计算方法,今天的任务是探究勾股定理公式如何得到?教师引导学生从观察勾股定理的公式特征入手,思考勾股定理的公式中c2、b2、a2的几何意义,并在学生的回答基础上继续总结提示——若要完成证明需要借助三个面积分别为c2、b2、a2的正方形。老师提供一种证明思路,同学们完成证法一的证明过程。
3.自主探究。学生提出勾股定理公式中的c2可以表示以c为边长的正方形面积。a2+b2=c2就是表示两个正方形面积相加等于第三个正方形。并根据自己的理解完成课堂导学案中证法一。
课堂观察
将a2、b2、c2赋予几何意义时,学生先回答a2的几何意义是边长为a的正方形,通过引导之后正确说出a2的几何意义可以表示边长为a的正方形面积。接着很顺利地回答b2、c2的几何意义。
——合作探究,小组展示
1.拓展延伸。以拓展知识面、提高学生对本节内容的重视为目的,展示2002年数学家大会会徽即赵爽弦图。教师对勾股定理在数学中的重要地位进行介绍,其原因之一在于定理证明的多样性。
2.合作学习。在教师的提示、小组的讨论交流后,学生构造和分割图形的方式不同,证明a2+b2=c2的方式也不同。利用10分钟时间,每个学生在组内讲解自己的证明方法。
3.交流展示。在组内交流环节时,教师通过巡堂挑选学生代表上台讲解。学生的讲解方法有:总统证法(加菲尔德证法)、邹元治证法、尝试讲解欧几里得证法。
课堂观察
小组交流环节,学生都基本能够将自己提前学习的方法进行讲解。但有些小组因为提前准备不充分,讨论活动没有全面展开。此外还观察到部分基础较弱的学生在讨论交流阶段表现比较沉默。这个环节中值得一提的是李同学敢于尝试带领同学们一起理解欧几里得证法,当学生提前有准备时,即使面对难题,心中的畏难情绪也会相应降低。
(三)提出猜想,科学验证
1.通过计算,初步猜想。计算图2中的正方形面积,请学生提出自己的猜想。勾股定理是否只适用于直角三角形呢?图1中三角形的三边长是否满足a2+b2=c2?若不满足,请同学们提出不同三角形三边关系的猜想。学生在计算后认为钝角三角形中(图2左)a2+b2>c2,在锐角三角形中(图2右)a2+b2<c2。
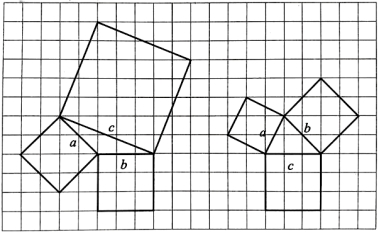
图2
2.针对猜想,科学验证。学生对以c为边长的正方形进行分割后,计算面积尝试验证自己提出的猜想,以图1两种情况为依据肯定猜想的正确性。教师针对学生提出验证方式的不完备,及时纠正学生对于证明的错误认识,让学生体会证明需要在一般情况进行。
课堂观察
对于猜想的验证,学生回应非常积极。但是在选取验证的依据时,没有选择一个更具有一般性的依据。仅仅通过一种或两种特殊的情况就确定了猜想的正误。验证勾股定理的时候我们通过用非特定的长度构造图形的证明来实现,特殊的情况不能够严格证明。而验证钝角和锐角三角形三边情况时,学生借助了边长为已知长度的特定三角形。因此特殊的情况下成立不能证明在一般的情况下成立,若要证明还需要更加严密地论证。此外学生对于边长不能直接看出的正方形面积计算上还存在一些障碍,对“割补”的方法求解图形面积还不熟练。
(四)课堂练习,知识应用
1.课中练测。完成课堂练习册,核对答案后请学生讲解。
2.例题讲解。应用例题讲解。
课堂观察
在课堂练习时间课堂瞬间降温,学生都在埋头做题、抬头听讲,相对于刚开始的课堂少了些活力,同时学生的课堂反应也慢了下来。
(五)课堂小结,拓展延伸
1.内容小结。学生跟着教师一起回顾勾股定理的证明思路与过程,并且强调证明应更具一般性。
2.拓展延伸。教师横向拓展勾股定理相关知识。第一次数学危机的产生与勾股定理有关,同时中国是文献记载中最早发现和研究勾股定理的国家之一。从数学史的角度解析勾股定理出现的重要意义。
课堂观察
在讲述数学史中勾股定理的出现和它的重要地位时,学生的兴致较高。但由于课堂时间有限,教师没有拓展知识之间的关联,导致学生没有深入体会到这个定理的历史价值。
