四 教学过程设计
(一)学习前置,知难生疑
1.整理、反馈学生预习成果。教师对学生提交的课前探究任务,利用互动平台进行批改并整理。在课堂展示中肯定学生的尝试并从学生的疑难点或共性错误方面,提出本节课的问题解决目标。
2.回顾旧知,承接新知探究。从回顾特殊三角形角度之间的关系,自然衔接学生对于直角三角形三边关系的猜想与证明思路。
3.从数学史的维度引出定理。早在公元前19世纪,古巴比伦人就已经将他们对直角三角形三边关系的猜想定理记录在泥板上。公元前1世纪一本《周髀算经》中也记录了智慧的古人对直角三角形三边关系的认识。将课堂探究中的三角形图案复制于单位长度为1的方格纸上,分别以其中一条边为边长作一个正方形。让学生通过计算,进一步验证或更新自己的猜想。
设计意图
将本节课的探究内容前置,使得学生在尝试解决问题的预学阶段,生成个性疑难问题。课堂以学生的共性疑难问题为课堂探究切入点。接着从特殊的三角形三角关系出发,过渡到对特殊三角形的三边关系的思考。由熟悉的知识引向未知的知识,自然过渡降低学生对新知的畏难情绪。同时能够加强知识间的联系,便于学生形成更为系统的知识框架。最后带领学生从历史的维度了解数学,讲述前人在数学史上的研究进程,在拓展学生知识面的同时激活他们解决新问题的信心。
(二)分组验证,新课导入
1.合作学习。学生通过计算,进一步验证或更新自己的猜想。验证需要大量计算,学生在组内与组间分工计算,从运算的结果中归纳出直角三角形的三边关系规律。
2.互动点评。同学们利用教学平台,在班级内发布自己发现的规律。同学之间可以用点赞或评论的方式,表达自己与其他同学观点的异同。教师利用投屏功能,将学生在班级的讨论的互动过程呈现在大屏幕上。
3.规范表述。教师根据学生的描述,加以提示使得学生的表述规范化。最终得到勾股定理的定理文字表述与符号表述。
设计意图
对于方式重复但数据不同的计算,可以通过组间、组内分工合作加快速度。计算结果可以作为其他小组的验证依据,提高探究效率。但是对于勾股定理的猜想无须让学生一步步完全经历,只要他们敢于提出猜想并尝试用科学的方法验证即可。验证时,在思路的引导上可更具方向性,提示学生思考边长平方之间的数量关系。依据计算数据,从多个特殊的例子中总结规律,让学生初步体会从特殊到一般的归纳推理方法。课堂中信息化手段的使用,能够快速便捷地收集并记录课堂情况,形成课堂即时反馈。同时利用教学平台与投屏功能,使得学生的交流不再局限于小组内部。教学平台的评论功能,能够帮助培养学生主动交流、敢于表达的习惯。
(三)“争当小毕达哥拉斯”
——方法探究
1.方向引导。教师引导学生从观察勾股定理的公式特征入手,思考公式中c2、b2、a2的几何意义。为公式证明方式的探究与理解初步寻找方向。
2.拓展延伸。展示2002年数学家大会会徽即赵爽弦图,以会徽为证明图形进行证明。学生尝试利用面积法进行对代数式的恒等证明。尔后可针对会徽,叙述勾股定理的证明多样性确定了它在数学中的重要地位。
3.合作探究。探究活动以小组为单位展开,利用小组的知识力量探寻证明勾股定理的不同方法。为避免部分学生在短时间内无法思考出对正方形割、补、拼的新方法,教师可以提前为这部分同学准备好锦囊妙计——适合学生水平的证明引导,如给定明确的图形学生只需要根据条件证明代数式之间的恒等关系。已经完成证明的小组把书写的证明过程,借助平板拍照反馈到教学平台。
4.教师视导。在组内交流环节时,教师通过积极巡堂了解每个小组的进度与困难。同时,可以利用教学平台所收集的学生反馈提高巡堂效率。
设计意图
学生经历上一环节的计算,可能会提出他们对证明的一种认识:通过几次计算验证了这个定理是正确的,因此定理成立。那么教师需要教导学生,证明并非依据几个事实就能够完成,数学结论和证明具有一般性与普适性。引导学生只需要将他们最初的方向稍加修改——用一个三边未知的直角三角形求证。教师以锦囊妙计的形式对基础较弱的学生进行引导帮助,提高学生的课堂参与度与成就感,让每个层级的学生都能在课堂中学有所得。此外学生利用平板将证明方法反馈到教学平台上,不仅能够帮助老师在短时间内获得更多学生的课堂反馈,还可使教师更深入地了解学生在课堂中的活动情况。投屏可以让班级小组了解班级中的探究进度,对比自己的与他人的方法异同。利用互评功能,开展组间交流。
——思维展示
1.展示交流。小组推选代表展示本组的证明方法,同学们可以在教学平台中,为简洁清晰的证明方法点赞或提出建议。
2.分析补充。教师在小组展示后,及时将各组讲解的方法进行简单的对比分析,引导学生发现证明方法之间的联系,并可以适当补充数学史中的证明方法。利用几何画板,展示利用图形分割、拼补的“无字证明”——如刘徽的“青朱出入图”、意大利画家达·芬奇的证明方法等。
设计意图
让能力层级较高的同学进行方法讲解,能够锻炼学生的数学表达能力,帮助学生梳理思路。对学生的讲解方法进行对比时,教师不仅要分析方法间的异同,还需总结各种证明中体现的不同数学思想方法。教师的总结起到提炼升华的作用,可适当补充数学史中的证明方法,开阔学生的思维边界但需考虑到学生的普遍能力。其中“无字证明”的方法,能够直观地进行证明。但在实际操作中却容易因为度量的误差难以完美实践证明。因此可以几何画板准确度量、分割,以直观且较准确的方式将图片分割和拼补的过程直观地展示。通过知识拓展与历史故事补充,让学生从人文的角度观赏数学,感受数学的底蕴与魅力。
(四)学以致用,强化理解
1.课中练测及时反馈。完成导学案中课堂检测部分,利用教学平台收集选择填空题答题情况。课堂检测的拓展任务学生可针对自身的情况选择性完成。
2.利用反馈查缺补漏。教师利用学情统计功能,了解学生的答题详情后进行针对性讲解,及时查缺补漏。
设计意图
利用信息化手段收集学生选择填空题答案,并能够将答题情况及时且准确地反馈给教师。教师便可以利用收集到的准确数据,在课中针对性地解决学生的疑难点。其中课堂检测的拓展任务为学习欧几里得证法证明勾股定理。方法本身难度偏高,适合基础扎实乐于挑战的学生,增加思维水平高的学生在课堂中的收获。
(五)知识梳理,课堂小结
1.分享感悟,整理总结。学生分享本节课的所得所思,教师在学生的分享基础上,梳理本节课的主要内容与思想方法。
2.概述内容,留下思考。教师简述历史上勾股定理的发展历程并提出思考问题——只有直角三角形中的三边关系满足勾股定理吗?勾股定理的三边关系是否能在钝角三角形、锐角三角形中成立?若不成立请描述钝角三角形、锐角三角形的三边关系。
设计意图
课程结束前,通过学生分享的所思所得,来了解本节课学生的思维状态以及学生对于知识点的理解程度。凸显学生的主体地位。教师整理学生的思悟,完善本节课的知识脉络,使得教学内容更具连贯性与整体性。因为勾股定理引发了第一次数学危机,并且中国是文献记载中最早发现和研究勾股定理的国家之一。从数学史的角度不仅能了解中国人在数学上做出的努力和成果,提高民族自豪感与对自身学习的信心,还能了解勾股定理如何推动数学发展。了解数学史也是一个让学生从不同角度了解数学爱上数学的途径之一。最后一道思考题引发学生对勾股定理的深入思索,为下节课埋下伏笔。既深化对本节课的证明理解,同时也为学生全面理解勾股定理提供了一个清晰的视角。
附件 《勾股定理及证明》课前预学案
附件:
《勾股定理及证明》课前预学案
探究1.下图的直角三角形边长已知。请你通过运算,提出你对直角三角形的三边长度关系的猜想。(三角形定点在格点上,并且方格的边长为1)
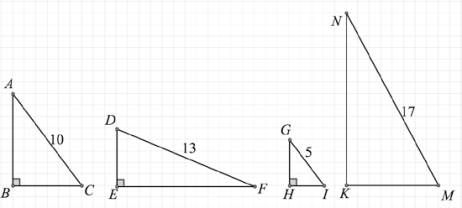
探究2.所有的三角形的三边长度都满足探究1中猜想的关系吗?请说说你的判断依据。
*探究3.数学中已有的关于直角三角形三边关系的定理是____________定理,又称为____________定理。关于这个定理有哪些故事和证明方法呢?
