三、因果预测法
因果预测法(Causal Forecasting Method),又称为“因果分析”,它是利用变量之间因果关系来进行预测的量化分析方法。在酒店需求预测中,常用的因果分析法包括简单线性回归、多元线性回归及非线性回归分析等。其中,多元线性回归和非线性回归分析应用的数学模型和计算过程较为复杂,通常作为酒店收益管理系统的内置工具使用,较少被收益管理团队作为人工分析方法使用。简单线性回归分析的原理和计算过程较为简便,运用得当的话,也具有较高的预测准确性。下面,就简单线性回归的原理和过程进行简要介绍。
简单线性回归,即一元线性回归分析。当因变量与自变量之间的因果关系呈现出线性变化时,就可以通过历史数据构造因变量与自变量的回归方程,进而通过将自变量的取值输入方程得到因变量的预测值。其主要步骤如下:
确认两个变量之间的因果关系。收益管理者要通定性分析、逻辑推理确认两个变量之间存在着因果关系。例如,某酒店管理团队发现,酒店的餐厅收入与客房出租率之间存在正向相关关系。即客房出租率越高,餐厅收入就越高。经过进一步分析发现,酒店餐厅早餐收入的90%来自住店客人,正餐收入的50%来自住店客人,故酒店餐厅收入与客房销售情况(可用客房出租率来衡量)之间存在着很强的因果关系。
初步确认两个变量之间的线性关系。酒店收益管理者可收集两个变量的历史数据,借助相关软件,如Excel、SPSS、Eviews制作散点图,观察散点图上点的分布情况,初步判断两个变量之间的因果关系是否以线性方式呈现。如果两者线性相关,则可以采用简单线性回归的方法来预测。
构造回归方程。当两个变量之间存在线性相关关系时,可借助相关软件构造回归方程:
式(4-3)中:y为因变量,x为自变量,a为线性回归方程的截距,b为线性回归方程的回归系数(即直线的斜率)。
拟合回归方程。借助相关软件,对回归方程y=a+bx的参数进行拟合,并得到决定系数R2。决定系数R2也称作“拟合优度”,其值大小表明了回归方程的拟合程度。例如,R2=0.8360,则表明在所构造的回归方程中,因变量83.60%的变化可以通过自变量得到解释。显然,R2越接近于1,回归方程的拟合优度越高。换言之,R2越接近于1,因变量与自变量之间的线性相关程度越高,越适合采用线性回归方程拟合;R2越接近于0,因变量与自变量之间的线性相关程度越低,越不适合采用线性回归方程进行拟合。
进行预测。当所构造的一元线性回归方程具有较好的拟合度时,即可用其进行预测。将未来某期的自变量取值输入回归方程,即可得到对应的因变量的预测值。
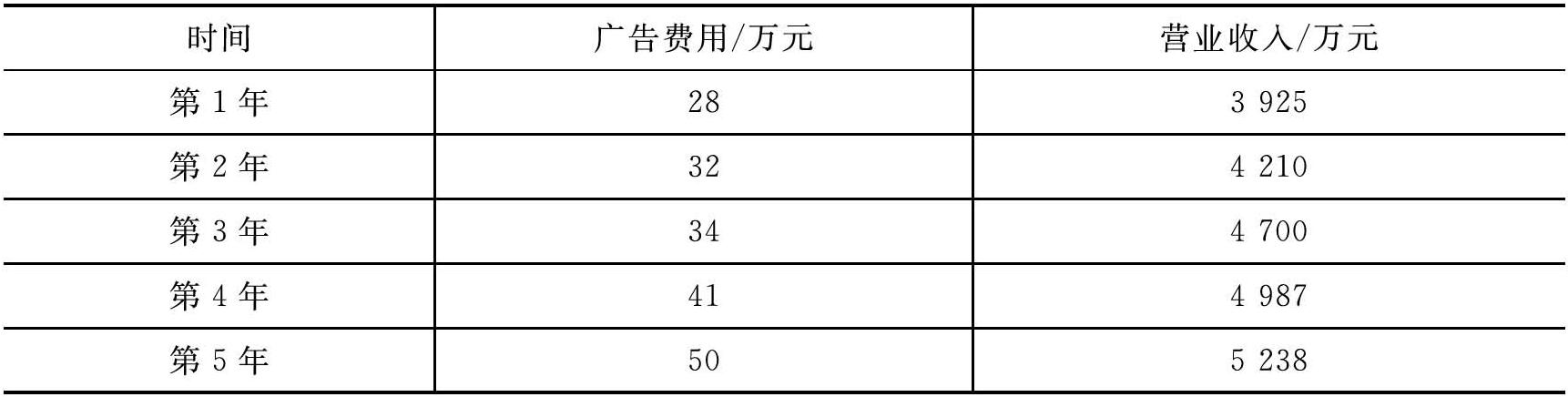
表4-22是某酒店过去10年的广告费用投入和营业收入情况。酒店收益管理团队发现,在过去10年中,酒店营业收入和广告费用都是逐年增加的,因而推断:营业收入的增加与广告费用投入有着密切关联。因为正常来讲,增加广告费用投入是有助于提升营业收入的。于是,他们试图构建酒店营业收入与广告费用投入之间的线性回归模型,通过该模型来预测下一年度的营业收入。
表4-22 某酒店过去10年的广告费用投入与营业收入
续表
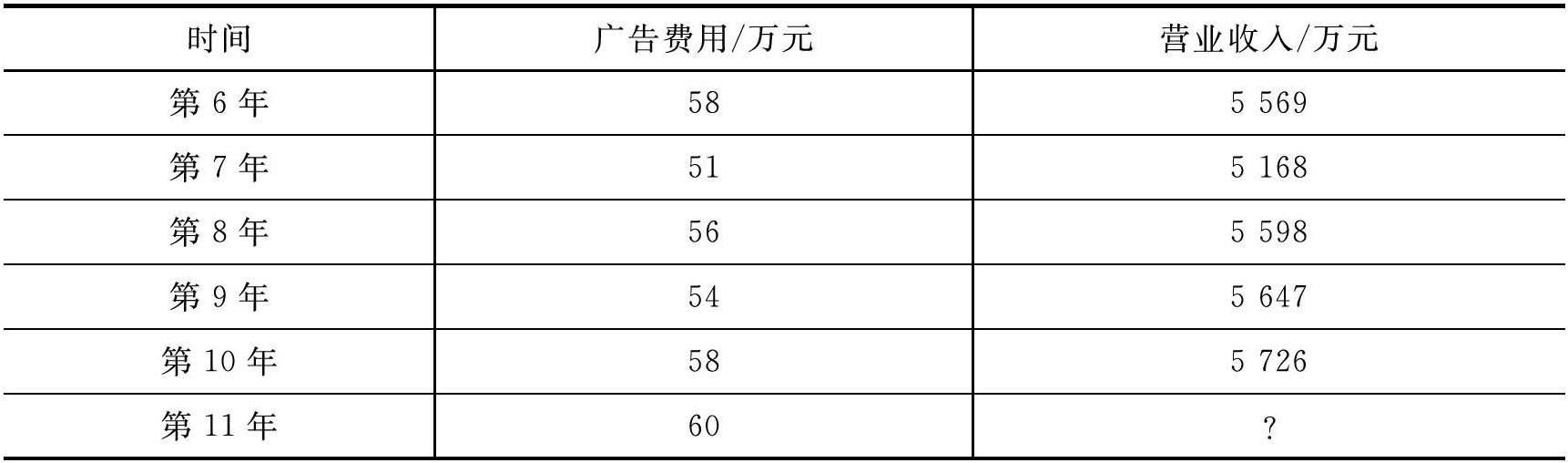
在确认营业收入与广告费用的因果关系之后,他们将过去10年的数据输入Excel表中,制作散点图(见图4-1),发现营业收入与广告费用组成的点在平面上呈线性分布,进而通过“添加趋势线”操作得到简单线性回归结果(见图4-2)。回归结果显示:营业收入y与广告费用x呈线性相关关系,直线的截距为2636.6,斜率为52.818;方程的决定系数R2=0.9357。由于方程具有很高的拟合优度,用该模型来预测下一年度的营业收入预计会有较高的可靠性。将第11年的广告费用60万元作为自变量代入方程,计算得到第11年营业收入预测值为5806万元。
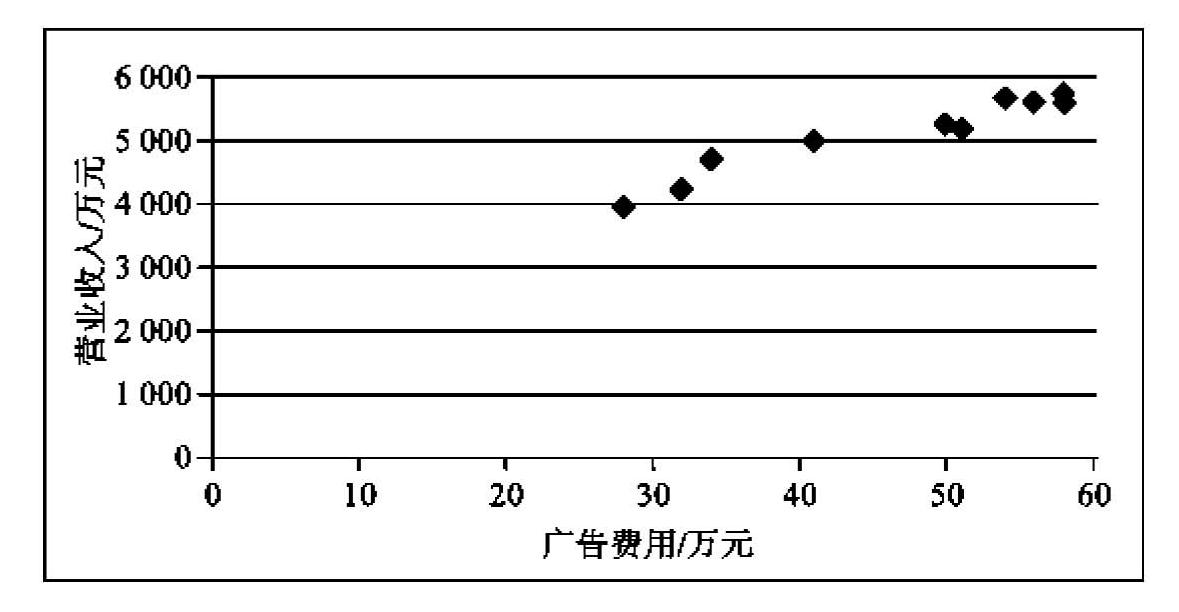
图4-1 Excel生成的散点图
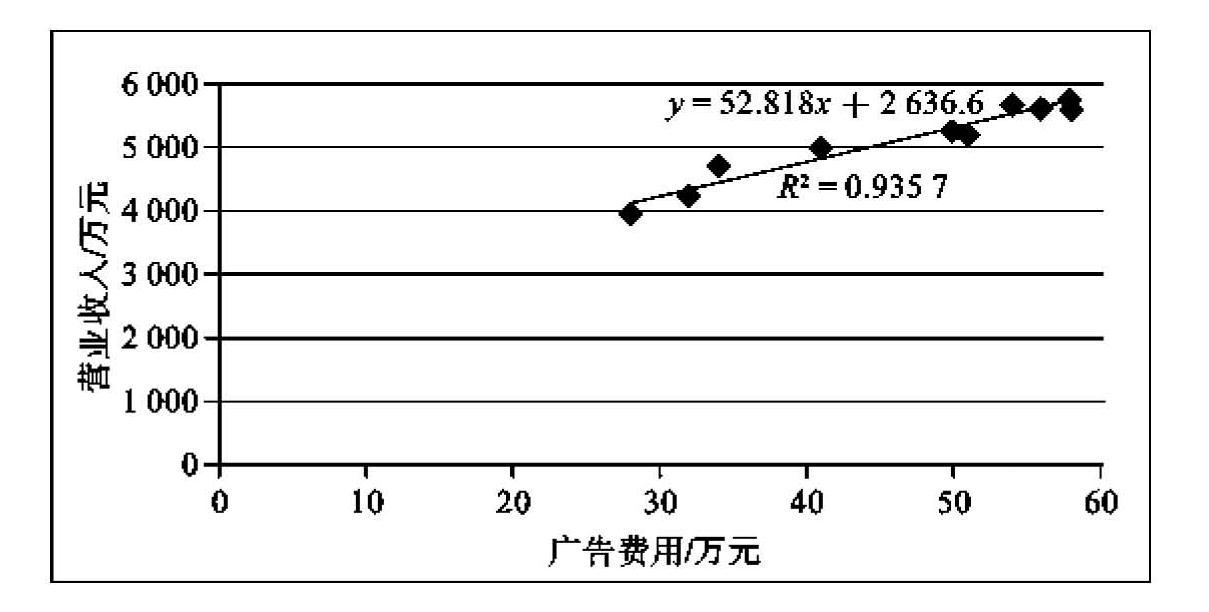
图4-2 Excel输出的简单线性回归结果
