预测准确性的衡量
预测准确性,又可称之为“预测精确度”,通常用预测误差的大小来衡量。而预测误差的衡量有多种方式,这里介绍酒店市场需求预测中最常用的三种误差衡量指标。
(一)平均绝对偏差
预测误差(Forecasting Error)是预测值与实际值的偏差。平均绝对偏差(Mean Absolute Deviation,MAD),又称为“平均绝对误差”(Mean Absolute Error,MAE),它是误差绝对值的平均值。采用这种方法来衡量预测的准确性,需要用特定时间内各期的预测值减去各期的观测值(实际值),得到各期的实际误差,然后对各期实际误差取绝对值,进而求取各期误差绝对值的平均值。该平均值即为该段时期内预测值的平均绝对偏差。
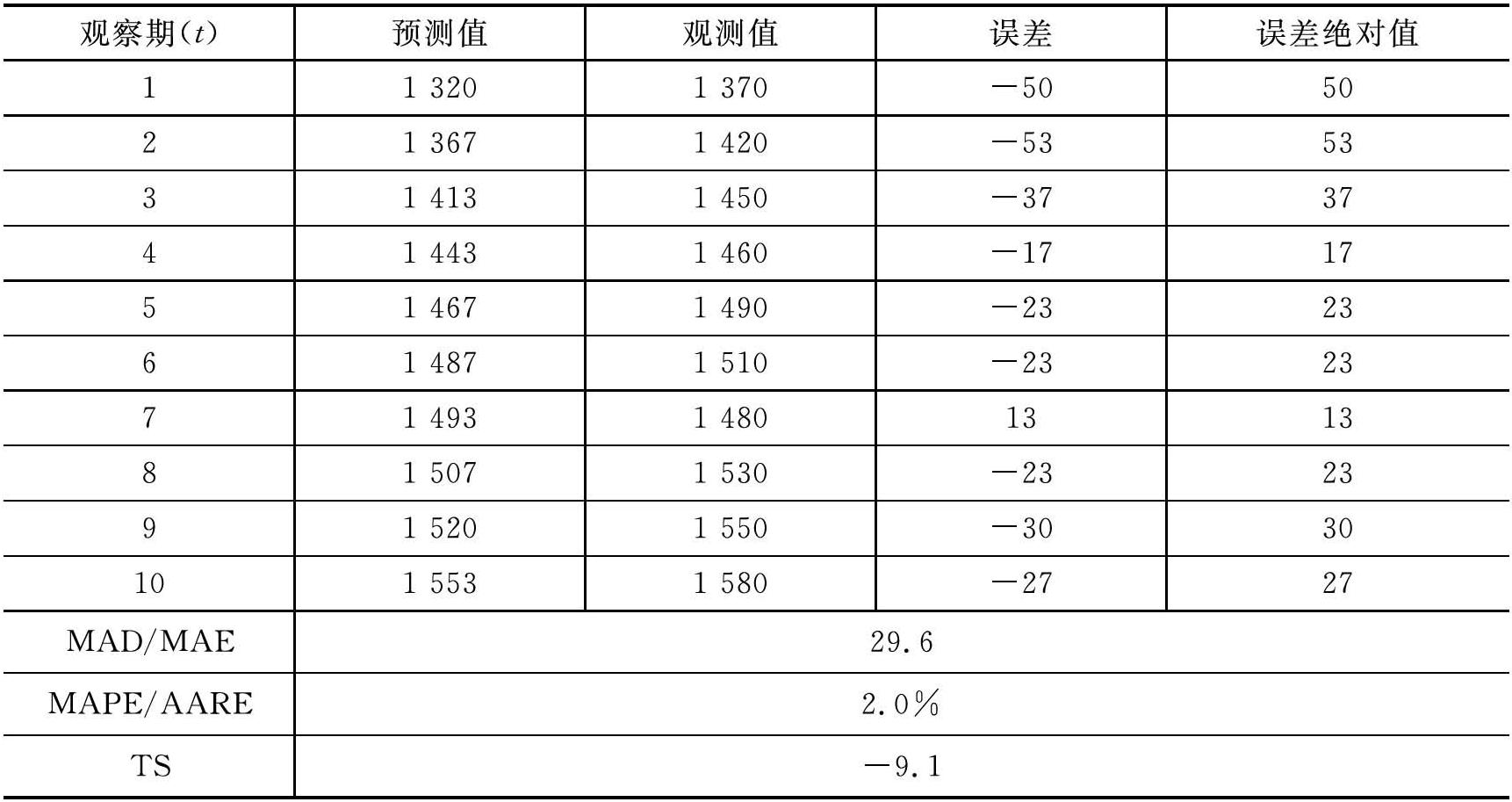
在表4-39中,第1~10期的实际误差分别为-50、-53、-37、-17、-23、-23、13、-23、-30、-27,因而各期误差的绝对值为50、53、37、17、23、23、13、23、30、27,由此可以计算得到第1~10期预测值的平均绝对误差为29.6。
表4-39 预测误差的衡量 单位:间
由于平均绝对误差可以避免正负误差相互抵消的问题,因而可以较为准确地反映实际误差的大小。就同一项预测而言,平均绝对误差越小,预测的准确性越高。然而相同大小的平均绝对误差,对于不同的预测而言并不必然意味着同等程度的准确性。因为预测的准确性不仅与平均绝对误差有关,而且与预测指标本身的取值也密切相关。因此,在实际工作中,人们还需要计算平均绝对百分比误差,以便反映预测误差相对预测指标取值的大小。
(二)平均绝对百分比误差
平均绝对百分比误差(Mean Absolute Percentage Error,MAPE),又称为“相对平均误差”(Average Absolute Relative Error,AARE),用以衡量平均绝对误差相对于预测指标观测值的大小程度。其计算过程为:先计算各期误差绝对值相对于当期观测值的大小(用百分比表示),再取各期误差百分比的平均值便可得到平均绝对百分比误差。或者,先计算过去各期的平均绝对误差和各期观测值的平均值,然后用平均绝对误差除以各期观测值的平均值得到平均绝对百分比误差。
在表4-38中,第1~10期的平均绝对误差(MAE)为29.6,而第1~10期观测值的平均值为1484,故而很容易得到第1~10期的平均绝对百分比误差(MAPE)为2.0%。就酒店市场需求预测而言,2.0%的相对偏差,可以认为是一项精确度很高的预测。
(三)跟踪信号
跟踪信号(Tracking Signal,TS)是误差的总和与平均绝对误差(MAE)之比,用以衡量预测误差的方向。
在表4-38中,第1~10期误差的总和为(-50)+(-53)+(-37)+(-17)+(-23)+(-23)+13+(-23)+(-30)+(-27)=-270,故第1~10期的跟踪信号为:
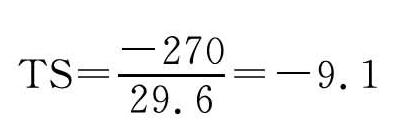
跟踪信号是一个负值,说明该酒店在过去10期的预测中总体上偏保守,在今后的预测中可以往更积极的方向调整。
综上,我们学习了平均绝对偏差、平均绝对百分比误差和跟踪信号三个预测误差衡量指标。平均绝对偏差可用于酒店预测误差的纵向比较,通过纵向比较可以了解酒店当前预测相较于以往预测的准确性是否有所提升。而且,平均绝对偏差也是计算平均绝对百分比误差的基础。平均绝对百分比误差不仅可以用于单一酒店的误差分析,而且也可以用于不同规模或不同区域的酒店之间的比较,可用于酒店集团评价下属酒店预测工作的准确情况。
