板块二 新知探究:明晰
活动一:画一画,说一说
1.跳绳、踢毽子比赛(不重复)。
三(1)班参加跳绳和踢毽子比赛的学生名单

三(1)班参加跳绳和踢毽子比赛的一共有多少人?
师:请大家仔细读题,想一想,参加两项比赛的一共有多少人?
生:12人。
师:你是怎样列式的?
生:7+5=12(人)。
师:不错!看来这道题没有难住大家!
2.重复。
三(2)班参加跳绳和踢毽子比赛的学生名单

三(2)班参加跳绳和踢毽子比赛的一共有多少人?
师:这是三(2)班参加这两项活动的情况!请大家仔细读题。你认为三(2)班参加两项比赛的一共有多少人?
生:还是12人。
师:你有不同意见,你为什么不同意呢?
生:有重复的,所以肯定不是12人。
师:你真会观察!
师:哪些名字重复啦?现在请大家想想办法,应该怎样设计就能看出哪些名字重复了呢?
师:请动手画一画、写一写,然后在小组内互相介绍自己的想法。
3.交流汇报。
师:哪位同学愿意来分享自己的想法?
(生出示。)
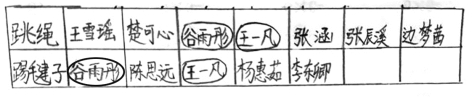
师:请你们小组派一位代表上来!把你的作品展示给大家,说一说你是怎么想的?
生:可以在表格里找到重复的名字,直接圈起来,看看重复了几人,再数出一共有几人,说明参加比赛的就有几人。
师:你是用圈一圈的方法找到了重复的,不错!还有不同的方法吗?
(生出示。)
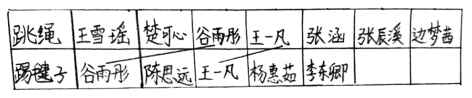
师:请你来!把你的作品给大家展示一下,说一说你是怎么想的?
生:把参加两项比赛的人都写出来,把相同的名字连起来,找到两项比赛都参加的有2人。用参加跳绳的7人,加上参加踢毽子的5人,再去掉2个重复的,所以答案是10人。
师:你是用连一连的方法找到了重复的,你说得真清晰!声音再大一些就更好啦!还有不同的方法吗?
(生出示。)
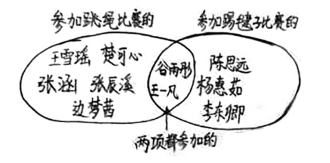
师:你还有想法,请你来!把你的作品给大家展示一下,同学们请看!这个方法很有创意,给大家说一说你是怎么画的,每一部分分别表示什么?
生:我是画了两个圆,左边是参加跳绳的,右边是参加踢毽子的,把两项比赛都参加的人移到一边,两个圆里都有这2个人的名字。可以把这部分重叠起来,名字只出现一次,可以看出只参加跳绳子比赛的有5人,两项比赛都参加的有2人,只参加踢键子比赛的有3人,一共有10人。
师:大家听明白了吗?哪位同学也用了这种方法?你们预习得真好!自主学习的能力真强!
师:老师也带来一幅这样的图,谁能看着这幅图再给大家解释一下?
(生回答。)
师:你说得真清楚,声音也洪亮,大家把掌声送给他!自己再说一遍吧!
现在老师考考你!左边月牙图表示什么?(只参加跳绳比赛的)(板书:只)“只”用得好!右边月牙图表示什么?(只参加踢毽子比赛的)(板书:只)中间的重叠部分表示什么?(你用到了“既……又……”这个关联词,表述得真准确!)(板书:既……又……)谁能用这个关联词再说一遍,请你来说,你今天学得真好,为你点赞!
师:刚才这幅图谁知道它是什么图呢?你知道,它叫维恩图,又叫集合图,你怎么知道的?你是通过读书知道的,读书丰富了你的视野;你是听家长说的,真是个有心的孩子。老师也带来了一个这样的知识,请听!(播放维恩图的知识)
师:老师从你们专注的眼神里发现,你们很佩服维恩这位科学家。的确,用维恩图表示形象又直观。这就是今天我们要研究的“集合”问题,齐读课题。
师:刚才大家用了圈一圈、连一连、画一画的方法找到了一共的人数,老师发现同学们解决问题的能力真强!能用这么多不同的图示来表示,你们真了不起!
设计意图:这个环节的设计,通过圈一圈、连一连、画一画的活动,在对比中感知集合的简洁和清晰之美,激发学生学习集合知识的欲望和增强探究意识。同时渗透对学生数学文化的熏陶。
活动二:算一算,说一说
1.(出示)这道题要求算出两项总人数,该怎么列式呢?请大家把算式写在练习本上,然后在小组内说一说为什么这样列式?(小组交流)
2.小组汇报。
师:请第2小组介绍你们的方法!
1号:算式是7+5-2=10(人),7表示参加跳绳的人数,5表示参加踢毽子的人数,2表示既参加跳绳又参加踢毽子的人数。
师:解释得不错!你是用参加跳绳的人数+参加踢毽子的人数-重复的人数,求出总人数。
2号:5+3+2=10(人),5表示只参加跳绳的人数,3表示只参加踢毽子的人数,2表示既参加跳绳又参加踢毽子的人数。
师:你是用只参加跳绳的人数+只参加踢毽子的人数+重复的人数,求出总人数。这样的算式也不错,每一部分解释得很清楚。
3号:7-2+5=10(人),7表示参加跳绳的人数,2表示既参加跳绳又参加踢毽子的人数,5表示参加踢毽子的人数。
师:这个小组真会动脑筋,想出了这么多的方法,真厉害!谁还有补充?
4号:7+(5-2)=10(人)。
师:你认为还可以这样列式,请问5-2表示的是哪一部分呢?(只参加跳绳的人数)有道理!
师:大家想出了这么多的方法,这几种方法你最喜欢哪一种方法呢?说说理由!
师:你说,你喜欢第一种,你也喜欢第一种,大部分同学都喜欢第一种,因为这种方法更好理解。再把第一种方法在同桌间互相说一遍吧!
设计意图:这个环节的设计是应用集合思想解决问题,体会集合圈简洁明了的特点,体现数学的简洁美。初步培养学生的建模意识和能力,增强用多种方法解决问题的意识。
