板块二 新知探究:明晰
1.认识内角、内角和。
(1)指一指。
师:谁来指一指这个三角形的内角(一生指),请看他是这样指的,大家看他指对了吗?
生:对了。
师:你给大家说一说什么是三角形的内角?
生:三角形的内角就是三角形里面的角。
师:三角形里面的角就是三角形的内角,说得不错!
(2)标一标。
师:那现在请在三角形中标出内角。标好了吗?请看他是这样标的:∠1、∠2、∠3。把你标的内角举起来让大家看一看,你标出了几个内角呢?
生:3个。
师:看来每个三角形里都有3个内角。
(3)说一说。
师:什么是三角形的内角和呢?
生:∠1、∠2、∠3加起来就是三角形的内角和。
师:三角形里三个内角度数的和就是三角形的内角和。所以,要求三角形的内角和可以把这三个角∠1、∠2、∠3加起来。说得真棒!你真会思考。
师:三角形的内角和到底是多少度?
生:我认为它们的内角和是180°。
生:我认为它们的内角和约是180°。
师:怎样验证三角形的内角和是180°?你准备用什么方法验证?
生:用量一量的方法。
生:也可以用撕一撕、拼一拼的方法。
师:你们的方法真是多种多样,下面我们一起来探究吧!
设计意图:明确三角形“内角”和“内角和”的概念,是学生进一步探究新知的前提。让学生大胆地“猜一猜”,激发学生探究数学的兴趣。
2.举例验证。
(1)剪一剪。
师:请小组合作,拿出你们准备好的三角形,任选一种方法,边操作边交流你们的思考过程吧!
(交流汇报。)
生:我用的是锐角三角形,把∠1、∠2、∠3撕下来拼成一个平角,平角的度数是180°,所以三角形的内角和是180°。
生:我用的是直角三角形,把∠1、∠2、∠3撕下来拼成一个平角,平角的度数是180°,所以三角形的内角和是180°。
生:我用的是钝角三角形,把∠1、∠2、∠3撕下来拼成一个平角,平角的度数是180°,所以三角形的内角和是180°。
师:你们是用剪一剪、拼一拼的方法,把三角形的三个内角剪下来,拼在一起,拼成了一个平角,平角是180°,说明三角形的内角和是180°。真了不起,能借助平角的度数来推想,你们真会思考!还有其他方法吗?
(2)折一折。
师:哪组还有不同的方法?
生:我用的是折一折的方法,把钝角三角形的三个角分别往里折,可以拼成一个平角。
生:我也是用折一折的方法,我用的是锐角三角形,也能拼出一个平角。
师:你们是用折一折、拼一拼的方法,你们是把三角形的三个角折下来,拼在一起组成一个平角。也是借助平角的度数来推想,证明三角形的内角和是180°。你们这样折真是太聪明啦!
(3)量一量。
师:还有呢?你们组来说吧!
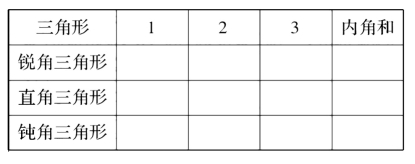
生:我们是用量一量的方法,发现三角形内角的度数相加刚好是180°。
师:你们是用测量的方法,这是他们的测量结果,探究出了三角形的内角和就是180°。其他组有补充吗?第三组你们有补充!
生:我们量出的结果不同,我们量出的三角形的内角和是181°和179°。
师:你们测量的三角形的内角和分别是181°、179°。这是怎么回事呢?你说。
生:因为测量时会有误差。
师:你还有什么想说的?哦,你是直接用三角板验证的。你们通过探究明白了三角形的内角和为什么是180°。
师:(小结)刚才我们通过量、剪、折等方法,验证了不同类型的三角形的内角和都是180°,后一种方法重在计算,前两种方法重在转化。虽然方法不同,但都可以帮助我们探究出:三角形的内角和是180°。同学们可真了不起,你们通过动手操作,验证了“三角形的内角和是180°”这一结论,请大家一起来读一遍吧!
师:通过刚才的验证,你想对大家说什么?
生:我发现每个三角形的内角和都是180°。
师:你认为任何一个三角形的内角和都是180°。你真会思考,只要是三角形,内角和就是180°,与它的形状、大小都没有关系。
通过学习,大家对今天的知识还有疑问吗?
生:四边形的内角和是多少呢?
生:四边形、五边形、六边形的内角和怎样验证呢?
师:请大家带着这些问题课下继续探究吧!
设计意图:“动手实践、自主探索”是学习数学的重要方式,也是尝试探究学习的主要方法。学习过程中把学生推到主动学习的位置,让他们利用已有的知识经验尝试解决问题,获得新的体验和感受。尽管有时他们的理解是片面的、不完整的,但在与同学的思维互动中,在教师的点拨启发下,数学模型的建构不断完善、不断科学。学生也会在思维的碰撞中,主动地进行思考、验证、推断,发散思维和创新意识就会逐渐培养起来。
