板块二 新知探究:明晰
活动一:说一说
师:同学们,这节课我们学习循环小数(板书课题)。根据你的理解,你认为“循环”是什么意思?
生:没有尽头。
生:永远也不结束。
师:对,大家理解得差不多。字典上的答案是:所谓循环,就是指事物周而复始地运动或变化。(课件出示)
师:生活当中,你见到过哪些循环现象呢?
生:春夏秋冬的轮流。
生:钟表上指针的转动。
生:红绿灯的交替出现。
生:每周从周一到周日。
师:你们太棒了!真善于观察生活,找到了这么多循环现象。老师也找到了一些。(课件出示)白天黑夜的交替、四季的轮回等。
师:在二年级我们学习过找规律的题,请看:▲▲▲( )( )( ),怎么填?
生:填▲。
师:如果后面有无数个空,是不是循环?
设计意图:解释“循环”,找生活中的循环现象,为新课学习做好铺垫,体现数学与生活的密切联系。同时回忆“找规律”的知识,建构起新旧知识之间的联系。
活动二:算一算
师:计算下面三道题,做完后在小组内交流你们的发现。
(出示35÷14、35÷15、35÷16。)
生:通过计算我们发现第一道题能除尽,得2.5。第三道题除尽了,但是不好算,得2.1875。
生:第二道题除不尽,得2.333……再往下除还得3,不知道怎么记下来结果了。
生:我们通过讨论和看书知道,像第二道题的得数,就叫循环小数。因为3一直不断重复出现。
师:你们怎么知道再往下除还是得3呢?说说你的发现。
生:因为我们发现计算时一直都是余5。
生:所以我们认为不用再算了,除到商重复出现3的时候。
生:除到余数重复出现5的时候。
师:第二道题的结果该怎么记录呢?谁有办法?
生:2.333……
生:2.3。
生:2.(3)。
师:你们最喜欢谁的设计?为什么?书上告诉了我们记录的方法,请大家阅读课本33页的内容,边读书边思考边批画。
生:(课件同步演示)第一种,写三遍3然后写省略号;第二种,写一遍3,然后在3的头上写一个小圆点,表示3重复,循环节是3。
师:你的学习能力真强!从书中找到了相关的知识,还知道了循环节。同学们,哪种记录比较简便呢?
生:第二种记录简便,循环节一眼就能看出来,很清晰。
师:这个数怎么读呢?
生:读作2.3循环。
生:我认为不对,不知道哪个数字循环。我觉着读作2.3,3循环。
师:你们觉得谁读得对呢?我们一起读一遍吧。
设计意图:设置三道形式接近的除法笔算,让学生从中发现问题,既巩固了小数除法的计算,又为循环小数的出现找到了载体。通过计算、小组交流中的碰撞,引发学生对除不尽的原因的思考,为循环的原理及循环小数的教学做好铺垫。循环小数的表示形式,让学生从课本上找答案,而不是老师告知,体现了阅读的数学思想。同时充分激发学生的积极性,深层次理解循环小数的表示方法。
师:我们再来计算两道题,男生做第一道,女生做第二道,做完后注意检查,然后思考你们的发现。
28÷18= 78.6÷11=
生:我做的是第一题,商是1.555……
生:我有不同的记录方法,记作1.5,5循环。
生:我做的是第二题,商是7.1454545……
生:我记录的结果是7.145,45循环。
师:同学们的计算能力真强,学到的知识能够活学活用。那么,通过这两道题的计算,你有什么发现?
生:第一道的商的循环节是一位,第二道的商的循环节是两位。
生:也有可能是三位或三位以上。
师:你们真善于观察!循环节不止一位时,我们计算时需要特别细心,也考验着我们的耐心。
设计意图:再次计算两道题,一是练习循环小数的两种表示方法,同时丰富循环小数的内涵。循环节可以是一个数字,也可以是两个或多个数字。
活动三:分一分
师:通过刚才五道题的计算,你知道什么是循环小数了吗?
生:一个小数的小数部分,从某一位起,一个数字或几个数字依次不断地重复出现,这样的小数叫作循环小数。
师:在这句话里,哪些是关键字?
师:小数部分,依次不断,重复。
师:我们把这句话齐读一遍,注意把关键词读得重一些。
师:同学们,刚才这五道题,你能把它们的结果进行分类吗?
生:我把结果分为两类,2.5、2.1857是有限小数,2.3……、1.5……、7.14545……是无限小数。
生:我觉着小数分为三类:有限小数、无限小数、循环小数。
师:你们同意谁的观点,同桌商量一下。
生:我们同意分两类,因为循环小数就属于无限小数。
生:对,我们也同意,循环小数是无限小数的一种,还有一种是不循环的,像圆周率,虽然位数是无限的,但是找不到循环节。
师:有理有据,老师也同意你的观点。你现在背到小数点后面第几位了?
生:背到了小数点后面第100位。
师:请把它们之间的关系用图示表示出来。
(生出示。)

(生出示。)
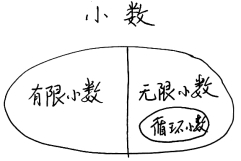
设计意图:逆转教材,由教材上最后给出有限小数和无限小数分类为前置,先行分类为有限小数和无限小数,再由无限小数中分出无限循环小数和无限不循环小数,体现由大到小的分类逻辑,符合学生认知规律。同时,把学习主动权交给学生,体现以学生为中心的课标理念。
