板块二 新知探究:明晰
活动一:数一数
师:通过课前预习,谁知道平行四边形的面积怎么求?
生:平行四边形的面积=底×高
师:对。根据前面的学习经验,我们在测量长度时是借助小线段来度量的。想一想,学习长方形、正方形的面积时,我们是借助什么来度量的?
生:借助小正方形来度量。
师:是的,平行四边形的面积怎样借助小正方形来探究呢?请大家拿出学具试一试。
活动要求:
1.在方格纸上数一数,把结果填在表格里。
2.思考:你是怎样数的?
3.观察表中的数据你发现了什么?
(先独立探究,然后三人小组交流方法,选代表汇报。)
生:(上台展示数方格的方法)边操作边讲解:我是先数满格,有20个满格;再数半格,共有8个半格,按4格来算,所以平行四边形一共有24个小格,它的面积也就是24平方米。
生:我有不同的数法。因为题目要求不满1格都按半格计算,我担心会有误差,所以我把平行四边形左边的三角形整体平移到了右边的空缺部分,发现能组成一个长方形,正好能得到24个满格,数方格也更方便了。
师:你们想得真周到,不但数出了平行四边形的面积,还解决了可能存在误差的情况,真会学习。
在方格纸上数一数,然后填写下来。(一个方格代表1m2,不满一格的都按半格计算。)(录视频)
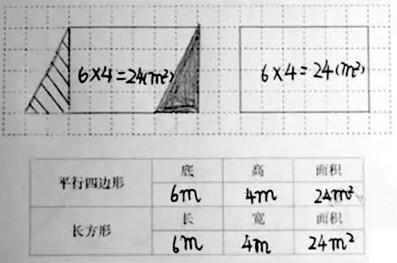
(1)仔细观察,比较表格中的数据,你发现了什么?
(2)大胆猜想,平行四边形的面积=____×____。
答:我发现长方形的长等于平行四边形的底,长方形的宽等于平行四边形的高。
师:仔细观察表中的数据,你发现了什么?
生:我发现平行四边形的底和长方形的长相等,都是6米,平行四边形的高和长方形的宽相等,都是4米,平行四边形的面积和长方形的面积相等,都是24平方米。
师:你观察得真准。通过观察、发现,大家都提出了自己的猜想:平行四边形的面积等于底乘高。这是通过数一个平行四边形的数据得到的,是不是每一个平行四边形的面积都等于底乘高呢?
设计意图:学生根据前面探究长方形、正方形面积的经验,借助数方格的方法,初步感知平行四边形与长方形之间的联系,通过动手操作不断发现问题和解决问题,并在与同伴的交流中调整数方格的方法。
活动二:剪一剪、拼一拼
师:如果求每一个平行四边形的面积都数方格,那就太麻烦了。试想不数方格,又该怎样计算平行四边形的面积呢?先独立思考,然后三人小组讨论交流,汇报想法。
活动要求:
1.将一个平行四边形剪拼成长方形。
2.利用学具画一画、剪一剪、拼一拼。
3.你能想到几种方法?
(小组合作,动手操作,播放音乐。)
(学生展示,汇报不同的方法。)
生:我是用剪拼的方法来求的。我先从平行四边形的顶点向它的对边画一条高,然后沿高剪开,得到一个直角三角形和一个直角梯形。再把三角形平移到右边,就得到了一个长方形,而平行四边形的面积没有变。
生:我是从平行四边形一条边的中间画高的,剪开之后,得到两个相同的直角梯形,通过平移,也得到了一个长方形。
生:平行四边形有两组对边,我从另一组对边画一条高,剪开再拼,也能拼成长方形。
(在黑板上展示每一种方法,总结操作步骤:一画、二剪、三拼,然后引导学生观察剪法,思考转化前后的联系。)
师:这么多剪拼方法,他们都把平行四边形转化成了长方形,仔细观察这些方法,它们之间有什么共同之处呢?
生:它们都是沿着高剪开的。
生:平行四边形有无数条高,任意一个平行四边形都可以沿高剪开,拼成一个长方形。
师:你真善于观察,你的发现很有价值。想一想为什么要沿着高剪?
生:沿高剪能得到直角,才能拼成长方形。
师:为什么一定要拼成长方形?
生:因为我们会算长方形的面积,不会算平行四边形的面积。
师:这个发现真了不起。这样我们就把新图形转化成学过的图形。这种转化思想是一种非常重要的数学思想,它可以帮助我们把新知识转化成学过的知识。
师:我们再横着观察,比较原来的平行四边形和转化之后的长方形,你发现了什么?
生:我发现长方形的面积等于平行四边形的面积,长方形的长等于平行四边形的底,长方形的宽等于平行四边形的高。
生:因为长方形的面积=长×宽,所以平行四边形的面积=底×高。
师:谁听懂他说的了,再来说一说。
(现场演示转化过程,能够强化重点,突破难点。)
(师用教具在黑板上演示,边操作边和学生一起说过程。)
师:这就是平行四边形面积的推导过程。请同学们拿起刚才拼剪的图形,边摸边给同桌说一遍。
(课件出示,一起回顾,进一步巩固强化公式的推导过程。)
师:如果用S表示平行四边形的面积,用a表示平行四边形的底,用h表示平行四边形的高,那么平行四边形的面积用字母怎样表示?
生:平行四边形的面积计算公式是S=ah
师:现在你知道求平行四边形的面积需要知道哪些数据呢?
生:必须知道底和高才能求。
生:而且是和底边对应的高。
师:你的补充很关键,求平行四边形的面积必须用一组对应的底和高相乘。接下来我们用填空的形式,再次梳理一下推导过程。
1.一个平行四边形可以转化成一个________,长方形的面积与原来平行四边形的面积________。
2.长方形的________相当于平行四边形的________,长方形的________相当于平行四边形的________。
3.因为长方形的面积=________,所以平行四边形的面积=________。用字母表示为________。

设计意图:第一个层次是剪拼转化的过程;第二个层次通过追问加深学生对知识的理解,凸显转化思想所起的重要作用;第三层次是找它们的关系。目的是让这节课更有层次性,更有思维深度。通过梳理等量关系的代换,培养学生的推理素养;通过观察、比较、总结、推理,建立数学模型,培养数学核心素养。
活动三:算一算
师:有了公式,我们就可以求任何一个平行四边形的面积了。
例:平行四边形花坛的底是6米,高是4米,它的面积是多少?
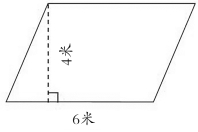
师:你会算吗?怎样书写呢?
生:先写公式,再把底和高的数据代入公式,计算出结果,写上答句。
师:学会了平行四边形面积的计算方法,快去帮小明家推荐一种合适的停车位吧!
(课件出示,求长方形停车位的面积需要知道什么?求平行四边形停车位的面积需要知道什么?学生独立解答。)
设计意图:例题教学,在学生充分明确公式的基础上,规范做题步骤,并与导入环节相呼应,用今天学的知识帮助小明家解决了问题。
