板块三 闯关练习:巩固
挑战一:选一选(练习十五第7题)
在能拼成三角形的各组小棒下面画“√”。(单位:cm)。

师:请同学们独立完成。(巡视指导)
师:谁来讲一讲?
生:第1组,3+4>5,能围成;第二组3+3>3,能围成;第三组2+2<6,不能围成;第四组3+3>5,能围成。
师:你讲得很清楚,谁还有补充?
生:我觉得只要两条短边之和大于最长边,就可以围成三角形。
师:真善于总结!
挑战二:想一想(练习十五第8题)
用下面6根小棒,你能摆出几种三角形?(单位:cm)
![]()
师:先独立思考,然后把你的想法和小组同学说一说。
师:哪个小组代表来讲一讲你们的想法?
生:我觉得2厘米长的小棒最多选1根,因为2+2<5,2+2<6。可以用2厘米、5厘米、6厘米长的小棒围成一个三角形,因为2+5>6;也可以用一根2厘米长的小棒和两根6厘米长的小棒,因为2+6>6;或者用一根5厘米长的小棒和两根6厘米长的小棒,因为5+5>6;还可以选三根6厘米长的小棒,因为6+6>6。一共能摆出4种三角形。
师:逻辑推理能力真强!掌声送给他!大家听明白了吗?谁再来讲一讲?
(生讲解。)
师:同学们,你们能应用“两短边之和大于最长边即可围成三角形”这个小窍门来解决问题,真是活学活用啊!
挑战三:用一用
(1)从小明家到学校有几条路可走?哪条路最近?
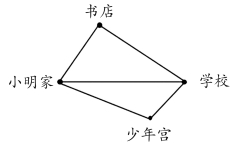
师:谁来讲一讲?
生:小明家到学校有三条路可走,中间的路最近。
师:你能用今天所学的知识来解释一下吗?
生:因为三角形的两边之和一定大于第三边,所以经过书店和经过少年宫的路都比直接到学校的路远。
师:看来数学知识是相通的,对同一个问题我们可以从不同的角度来思考。
(2)公路的两侧有A、B两个住宅小区(如图),现在要在公路上建一个公交站,让这两个小区的人到公交站的路线之和最短。公交站应建在什么地方?
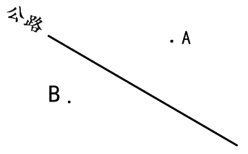
师:请同学们先自己想一想、画一画。(师巡视指导)
师:谁来讲一讲?
生:连接A、B两点,在线段AB和公路的交叉点处建公交站牌,这样两个小区的人到公交站的路线之和最短。
师:你还有疑问?是啊,为什么这样一连就是最短的呢?
生:如果把公交站牌建在其他地方,比如这里(在公路上画一个点C),ABC是一个三角形,因为三角形任意两边之和大于第三边,所以AC+BC>AB,这样就不是最近的了。
(学生用心聆听,自发鼓掌。)
挑战四:剪一剪
有这样两张纸条,怎样剪能围成三角形?(注意只能剪一次)

生:剪长的,如果剪短的,两边之和就小于第三边了。(课件动画演示)
师:是不是从任意位置剪都可以呢?
(生产生分歧,大部分认为可以,小部分认为不可以。)
师:你为什么认为不可以呢?
生:如果剪下的一小段纸条很短,和下面的短纸条的长度之和不大于剩余纸条的长度,就不能围成三角形了。
师:真善于推理!(课件演示)如果是两张同样长的纸条呢?
生:不行,因为这样两条线段的和就等于第三条线段了。
设计意图:通过层层递进的练习使学生能灵活应用“两短边之和大于最长边即可围成三角形”来判断是否能围成三角形,加深对三角形的三边关系的理解。并通过解决问题,着眼于生活应用,引导学生灵活运用数学知识解决生活中的实际问题。
