板块二 新知探究:明晰
探究一:倒数的意义。
1.先计算,再观察,看看有什么规律。
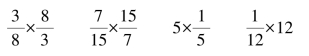
生:相乘的两个数的分子、分母正好颠倒了位置。
生:两个数的乘积都是1。
师:像这样,乘积是1的两个数互为倒数。因为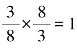 ,所以
,所以![]() 和
和![]() 互为倒数,就是指:
互为倒数,就是指:![]() 的倒数是
的倒数是![]() 的倒数是
的倒数是![]() 。
。
师:说一说算式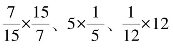 中的哪两个数互为倒数?
中的哪两个数互为倒数?
师:想一想,互为倒数的两个数有什么特点?
生:必须是乘积是1的两个数。
师:你能举出一组这样的例子吗?并说一说谁和谁互为倒数?
2.及时练。
说一说下面哪个算式中的两个数互为倒数?为什么?
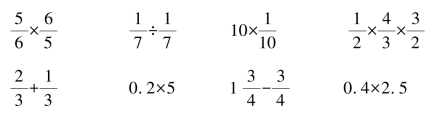
师:根据刚才的学习,什么样的数有倒数呢?
生:分数、整数和小数。
探究二:求一个数的倒数。
1.你能说出下面分数的倒数吗?并说说怎样想的。
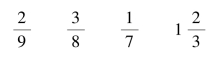
生:![]() 的倒数是
的倒数是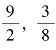 的倒数是
的倒数是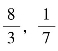 的倒数是7,
的倒数是7,![]() 的倒数是
的倒数是![]() 。
。
师:(小结)求一个分数的倒数,就是把它的分子和分母交换位置。
2.你能说出下面整数的倒数吗?并说说怎样想的。
8 10 1 0
生:8的倒数是![]() ,10的倒数是
,10的倒数是![]() ,1的倒数还是1,0没有倒数。
,1的倒数还是1,0没有倒数。
师:为什么1的倒数还是1,0没有倒数呢?
生:因为1和1相乘得1,0和任何数相乘都得0。
师:(小结)求一个整数的倒数,先把整数写成分母是1的分数,再把它的分子和分母交换位置。
3.你能说出下面小数的倒数吗?并说说怎样想的。
0.3 0.4 1.5
生:0.3的倒数是![]() ,0.4的倒数是
,0.4的倒数是![]() ,1.5的倒数是
,1.5的倒数是![]() 。
。
师:(小结)求一个小数的倒数,先把小数写成分数,再把它的分子和分母交换位置。
探究三:怎样求一个数的倒数?你有哪些收获?
设计意图:从一组有趣的乘法算式入手,留给学生充分的时间,让学生通过观察和计算直观地感受这组算式中两个因数以及积的特点,为总结倒数的概念做好了充分的准备。
观察算式,深入理解互为倒数的两个数的依存关系。通过猜想“什么样的数有倒数”这一问题,举例验证,发现不是所有的数都有倒数。在观察—猜想—验证的探究过程中,使学生的思维自然地迁移,在验证的过程中发现求一个数的倒数的方法,并将数的领域层层递进,由一般分数、整数到特殊的整数0和1,再到小数,从而全面掌握求一个数的倒数的方法。
