板块二 新知探究:明晰
活动一:制作冲突 感知重复
1.站位。
师:你为什么猜10人呢?
生:我觉得王相锦很厉害,两项比赛都有他,我们才会赢!
师:很有想法!我们班的选手们到底是谁呢?请大家看着名单大声把他们喊到台上。请参加“数学能手”比赛的小能手站在左边,参加“诗词能手”比赛的小能手站在右边。

师:同学们,小能手的站位对吗?
生:王相锦和郭妍应该站在左边。
生:不对,他们也参加了“诗词能手”比赛,应该站在右边。
生:不对,不对,他们两边都不能站。
师:为什么?
生:因为他们俩参加了“数学能手”比赛,也参加了“诗词能手”比赛,这两项比赛都参加了。
师:有道理,那他们应该站哪儿呢?
生:中间。
2.粘名。
师:现在这样的站位可以吗?
生:可以。
(三人小组合作:(1)按照他们的站位,把他们的名字粘到探究纸上。(2)说一说每一部分学生参加了什么项目。一组上台动手粘。)
师:请把掌声送给我们班的选手。
师:请你们组解释一下每一部分的同学都参加了什么比赛?
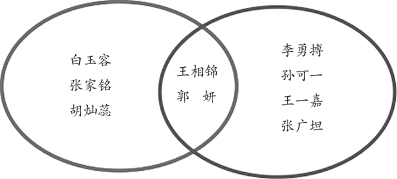
生:白玉容、张家铭和胡灿蕊只参加了“数学能手”比赛,所以他们的名字粘在左边;李勇搏、孙可一、王一嘉和张广坦只参加了“诗词能手”比赛,所以他们的名字粘在右边;王相锦和郭妍既参加了“数学能手”比赛又参加了“诗词能手”比赛,所以他们的名字粘在中间。
师:你讲得可真清楚,尤其是“只参加”“既参加,又参加”这几个词用得可真好!
师:刚才我发现你把郭妍和王相锦的名字放在讲台上一份,为什么?
生:因为郭妍和王相锦这两个名字出现了两次,重复了。
师:掌声送给合作有序、解说清楚的这一组。
师:咱们班参加比赛的有多少人呢?
生:9人。
师:不是需要11位选手吗?
生:因为有2人重复了,王相锦和郭妍既参加“数学能手”比赛又参加“诗词能手”比赛。
师:通过观察、比较,发现王相锦和郭妍重复参加了比赛。
设计意图:通过“站位”活动,给学生制造了一个小小的矛盾,让学生感知“重复”。在“粘名”活动中,让学生用语言精确地解释出每一部分选手参加的比赛项目,体现“重复”的重要性。
活动二:认识维恩图,初步感知集合
师:大家能不能用画图的方法,让人们一眼看出选手们都参加了哪些项目?
(生思考,师巡视,展示学生作品。)
师:请展示的小组,每组派一个代表讲解你们的方案。
(师重点展示用圈圈起来的作品。)
师:大家不要小看这两个圈,它们就是著名的维恩图。
(课件介绍:约翰·维恩(John Venn)是19世纪英国的哲学家和数学家,他在1881年发明了维恩图。)
(课件演示维恩图,单独的两个圈移动到一起,重复的部分重合。)
师:孩子们,你们太了不起来,和科学家想到一起去了。
师:(通过黑板上的图,总结出集合的概念)我们可以把参加“数学能手”比赛的5人看作一个整体,用红色的圈把他们圈在一起,在数学上,这个整体可以看作一个集合。我们把参加“诗词能手”比赛的同学也看作一个整体,用蓝色的圈把他们圈在一起,这个整体也可以看作一个集合。整个图表示三(14)班所有参赛同学的集合。(板书课题:集合)
三人小组组内交流:
(1)红色圈去掉中间部分,剩下的月牙表示什么?
(2)蓝色圈去掉中间部分,剩下的月牙表示什么?
(3)王相锦和郭妍到底属于哪个集合圈?
生:红色圈去掉中间部分,表示只参加了“数学能手”比赛的同学;蓝色圈去掉中间部分,表示只参加了“诗词能手”比赛的同学。王相锦和郭妍是既参加“数学能手”比赛又参加“诗词能手”比赛的同学。
(生回答,师板书。)
师(小结):通过刚才的学习,我们认识了维恩图,感知了集合思想。
设计意图:依据学生生成的资源,教师进一步抽象概括为集合圈,体现了知识的生成过程。通过对集合各部分元素的认识,让学生清楚地认识到三部分分别指哪些学生。体会到集合是否有交集,其实是分类标准决定的。
活动三:列式解决,加深理解
师:咱们班参加这两项比赛的共有多少人?这一问题,你会列式吗?可以结合维恩图想一想。
生:3+2+4=9(人)。
师:说说你的想法?
生:只参加了“数学能手”比赛的同学有3人,既参加“数学能手”比赛又参加“诗词能手”比赛的同学有2人,只参加了“诗词能手”比赛的同学有4人。
生:5+6-2=9(人)。
师:可以指着图给大家讲一讲你的想法吗?
生:参加了“数学能手”比赛的同学有5人,参加了“诗词能手”比赛的同学有6人。王相锦和郭妍是既参加“数学能手”比赛又参加“诗词能手”比赛的同学,他们的名字重复出现了2次,所以要减去一次。
师:他列的算式中的减2是把王相锦和郭妍去掉吗?减2表示什么?
生:不是把王相锦和郭妍去掉,是把他们重复出现的那一次减掉。
师:谁能再说一说生2的方法?
生:参加“数学能手”比赛的5人+参加“诗词能手”比赛的6人-重复出现的2人。
(板书:参加“数学能手”比赛的5人+参加“诗词能手”比赛的6人-重复出现的2人。)
师:我还有一种方法,5-2+6=9,谁知道老师是怎么想的?
生:老师是用只参加“数学能手”比赛的3人+参加“诗词能手”比赛的6人。
师:你还能想出别的方法吗?
生:6-2+5=9。
师:这么多方法,你最喜欢哪一种呢?
师:喜欢第二种方法的同学比较多,小组内再把第二种方法的意思说一说吧!
设计意图:在充分理解维恩图各部分的含义的基础上,引导学生用集合的思想方法解决问题。学生看着图示列算式比较容易,并说一说算式每一步表达的是哪一部分。本环节重点强调第二种方法,引导学生理解算式中的减2,是减掉重复的部分,加深学生对集合思想的印象。
