板块二 新知探究:明晰
活动一:动手操作,探索三角形边的关系
师:我们发现这三根小棒不能围成三角形,那么能围成三角形的三根小棒的长度到底有怎样的关系?
生:两根小棒的长度和大于第三根小棒。
师:同学们通过观察猜想出三角形的两边的和大于第三边。那么,大家的猜想是否正确呢?我们可以通过实验来验证,老师给同学们准备了一些材料:4厘米、5厘米、8厘米、12厘米的拼接条各一根,请同学们思考一下,任意选三根,有几种围法?(课件出示四根拼接条)
生:通过列举,我发现有4、5、8,4、5、12,4、8、12,5、8、12四种组合。
师:你真善于思考!下面我们就来动手围一围,齐读操作要求。(课件出示操作要求)
三人小组分工合作,两人操作,一人记录;围三角形时要注意首尾相连,边操作边交流。
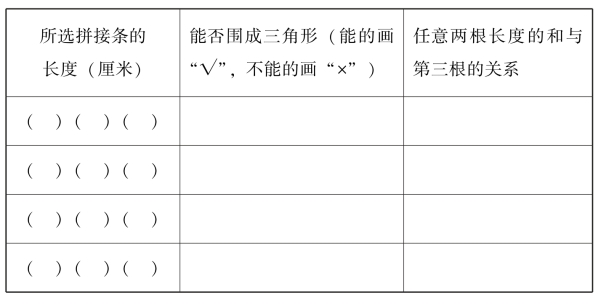
(学生小组合作,动手做实验,寻找规律。)
(师巡视指导。)
活动二:交流展示,深度理解三角形边的关系
师:同学们,现在我们用数据来说话,一起看看有什么发现?哪个小组来汇报?
(小组汇报。)
能围成三角形:
第一组:4厘米、5厘米和8厘米的拼接条能围成三角形,两根的和与第三根的关系是:4+5>8、4+8>5、5+8>4。
第二组:5厘米、8厘米和12厘米的拼接条也能围成三角形,两根的和与第三根关系是:5+8>12、5+12>8、8+12>5。
不能围成三角形:
第三组:4厘米、5厘米和12厘米的拼接条不能围成三角形,两根的和与第三根的关系是:4+5<12、4+12>5、5+12>4。(课件演示)
第四组:4厘米、8厘米和12厘米的拼接条也不能围成三角形,两根的和与第三边的关系是:4+8=12、4+12>8、8+12>4。(课件演示)
…………
师:这个小组分工合作,操作有序、讲解清晰、记录得也很完整,把掌声送给他们!同学们,再一起来看看不能围成三角形的情况,也有2+8>4、4+8>2、2+8>5、5+8>2(两边之和大于第三边)的情况,怎么就不能围成三角形呢?
生:有一种不符合就不能围成。
生:必须两条短边的和大于较长的边。
师:也就是说,必须满足任意两边之和都要大于第三边。(边说边板书)
设计意图:自主合作探究的学习方式充分尊重学生学习的主体性,有利于引导学生经历数学规律发现、数学结论形成的过程。对于三角形的三边的关系,通过让学生经历“实验—猜想—验证—发现”的全过程,引导学生带着问题去探究,使探究活动的指向更明确。用表格方式记录探究的结果,主要是为了更有条理地呈现具体的实验结果,为学生进一步观察、发现规律做好准备。学生通过猜想、操作、观察、分析、推理以及多媒体课件动态演示等活动,对三角形的三边关系逐步丰富了表象。由具体到抽象,扩展认知,体验收获。“什么情况不能围成三角形”“什么情况能围成三角形”这一重点和难点迎刃而解,较为顺利地探究和理解了三角形三边的长度关系。
活动三:练习提升,形成最优化数学模型
下列长度的三条线段,能否围成三角形?为什么?(单位:cm)
(1)6、7、8 (2)4、5、9
(3)3、6、10 (4)8、11、11
(学生独立完成,汇报交流。)
师:我发现有的同学只列了一个算式,也做出了准确的判断,能给大家讲讲你的想法吗?(课件演示)
生:我发现只要两条短边之和大于第三边,就能保证任意两边的和大于第三边,就可以围成三角形,所以只要看两条短边之和是否大于第三边即可。
师:下面我们就运用这一个快速判断的窍门进行一个课堂游戏——哪组线段可以围成一个三角形?男女生各选一个代表来PK,其他同学是他们的智囊团哦!
设计意图:再次优化,实际上也是引导学生打破刚才构建的数学模型,抓住问题的本质属性,只看两条短边与最长的第三边的比较,形成一个最优化的数学模型结构——两条短边之和大于第三边。
师:回顾刚才的探究活动,我们经历了怎样一个学习过程?引导学生梳理得出:大胆猜想—操作验证—得出结论。
师:同学们,你们学得怎么样呢?下面我们开始闯关练习!
