函数与极限
预备知识
1.常用的数学符号
（1）“∃”表示“存在”；
（2）“∀”表示“任意”；
（3）“∈”表示“属于”；
（4）“∉”表示“不属于”；
（5）“A⇒B”表示“如果命题A成立，则命题B成立”，或称“A是B的充分条件”；
（6）“A⇐B”表示“如果命题B成立，则命题A成立”，或称“A是B的必要条件”；
（7）“A⇔B”表示“A是B的充分必要条件”，或称“A与B等价”；
（8）
＝u1＋u2＋…＋un，即n个数ui（i＝1，2，…，n）求和；
（9）
＝u1u2…un，即n个数ui（i＝1，2，…，n）求积.
2.区间和邻域
高等数学中常用的数集是区间.它包括以下几种：
（1）［a，b］＝｛
≤x≤b｝，（a，b）＝｛
＜x＜b｝；
（2）［a，b）＝｛
≤x＜b｝，（a，b］＝｛
＜x≤b｝；
（3）［a，＋∞）＝｛
≥a｝，（a，＋∞）＝｛
＞a｝；
（4）（－∞，b］＝｛
≤b｝，（－∞，b）＝｛
＜b｝；
（5）（－∞，＋∞）＝｛
为任意实数｝.
邻域也是集合的一种形式，数轴（x轴）上点x0的δ（δ＞0）邻域定义为U （x0，δ）＝｛
－δ＜x＜x0＋δ｝；点x0的δ去心邻域定义为U （x0，δ）＝{
＜｜x－x0｜＜δ｝.其中，x0称为邻域中心，δ称为邻域半径，如图1－1所示.
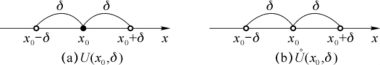
图1－1
3.常用的不等式
（1）绝对值不等式：－
≤a≤
；
（2）三角不等式：
（3）平均值不等式：设ai≥0（i＝1，2，…，n），则有
，当n＝2时，有
（4）柯西－施瓦兹（Cauchy－Schwartz）不等式：对任意实数ai，bi（i＝1，2，…，n），有
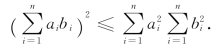
4.极坐标表示
中学数学讲到了平面直角坐标系，在该坐标系中，平面上任意一点P可用直角坐标（x，y）唯一表示；反之，任一有序数对（x，y）可以唯一地确定平面上的一点，也就是平面上的一点可由两个参数唯一确定.记点P到坐标原点的距离为ρ，线段OP与x轴正向夹角为θ，则有
如图1－2所示，平面上点P与有序数组（ρ，θ）（ρ≥0，0≤θ＜2π）一一对应，称（ρ，θ）为点P的极坐标.
显然，ρ＝a表示的是半径为a的圆：x2＋y2＝a2；θ＝
表示以原点为始点的沿y轴正轴方向的射线.直角坐标与极坐标之间的转换关系为
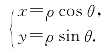
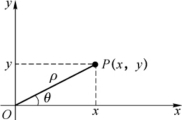
图1－2