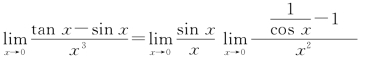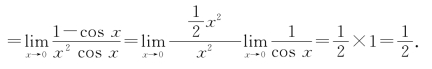无穷小的比较
本章第四节介绍了无穷小量的概念，即在自变量趋向于某个值时，极限为零的函数称为无穷小量，简称无穷小，记成o（1）.例如，当x→0时，函数x，x2，1－cos x，xsin
都是无穷小量；当x→＋∞时，函数
，e－x都是无穷小量；当x→1时，函数ln x，2x－1－1也都是无穷小量.已知两个无穷小量的和、差都是无穷小量，那两个无穷小量的商会怎样呢？
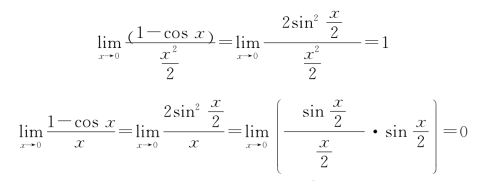
上述两极限反映了在x→0的过程中，1－cos x与
都是无穷小量，它们趋于零的“快慢”一致；x趋于零的速度显然要比1－cos x“慢些”.如何衡量这些无穷小量趋于零的“快慢”呢？
定义1 设
α（x）＝0，
β（x）＝0，那么：
如果
＝0，则称当x→x时，α（x）是比β（x）高阶的无穷小量，记为0
α（x）＝o（β（x）），（x→x0）；
如果
＝∞，则称当x→x时，α（x）是比β（x）低阶的无穷小量；0
如果
＝c≠0，则称当x→x时，α（x）与β（x）是同阶无穷小量；0
如果
＝1，则称当x→x时，α（x）与β（x）是等价无穷小量，记为0
α（x）～β（x），（x→x0）；
如果
＝c≠0，则称当x→x时，α（x）是β（x）的k阶无穷小量.0
注意 此处的x→x0可换成x的其他任何趋向，如x→∞，x→x0－，x→x0＋等.
例1 证明当x→0时，
证 令
－1＝t，则有
所以
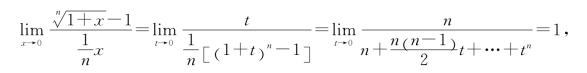
即有
x（x→0）.
等价无穷小量常被用于求极限、讨论函数的性质、近似计算等，是一个非常重要的概念.高等数学中常用的等价无穷小量如下：
当x→0时，有
sin x～x， tan x～x， ln（1＋x）～x， ex－1～x， 1－cos x～
例2 当x→0时，
（a＞0）是x的几阶无穷小量？
解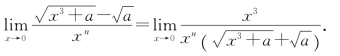
当n＝3时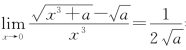
≠0，所以，当x→0时，
是x的3阶无穷小量.
等价无穷小量可用来简化极限的运算.
定理1 当x→x0时，若α1（x）～α2（x），β1（x）～β2（x），β1（x）≠0，β2（x）≠0，且
存在或为无穷大，则
证
例3 求
解 当x→0时，sin nx～nx，ln （1＋x）～x，所以
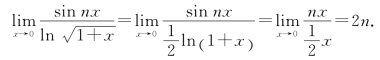
例4 求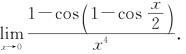
解 当x→0时，1－cos
，所以
有
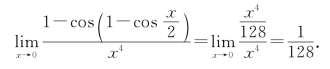
例5
解
