复合函数的求导法则
前面求出了一些基本初等函数的导数，而实际遇到的大多数函数是由基本初等函数复合而成的复合函数.下面介绍求导运算中的一个重要法则，利用它可以求出许多复合函数的导函数.
定理2（复合函数求导法则） 若函数y＝f（u）在点u可导，函数u＝φ（x）在点x可导，则复合函数y＝f［φ（x）］在点x可导，且
或
证 因为y＝f（u）在点u可导，由导数的定义得
即
其中
α＝0.此时有
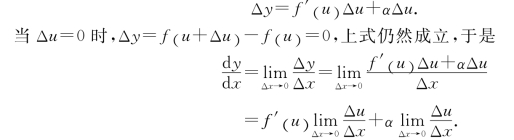
因为u＝φ（x）在点x可导，故在点x连续.于是，当Δx→0时，有Δu→0，且
α＝0.所以
上述求导法则又称作链导法则，它表示：复合函数y对自变量x的导数等于函数y对中间变量u的导数与中间变量u对自变量x的导数的乘积.此法则可推广到多重复合函数的情形.
设v＝v （x）在点x可导，u＝u （v）在点v可导，y＝f（u）在对应点u可导，则复合函数y＝f｛u ［v （x）］｝在点x可导，且
例9 设y＝
解 令u＝1＋x2，则y＝
，所以
例10 设y＝ln tan x，求
解 令u＝tan x，则y＝ln u.所以
例11 设y＝tan3 （lnx），求
解 令v＝ln x，u＝tan v，y＝u3，所以
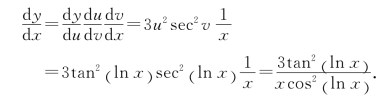
在熟练掌握了复合函数的链导法则后，可不必把中间变量写出来，只要分析清楚函数的复合关系就可直接求出复合函数对自变量的导数.
例12 设y＝
解
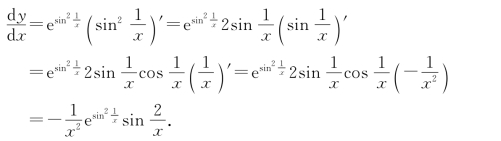
遇到多重复合函数的求导时，要毫无遗漏地逐次应用链导法则，由表及里，逐步求导，然后化简.
例13 求双曲函数的导数.
解
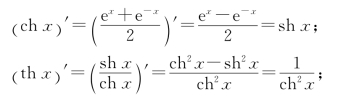
反双曲函数的导数：
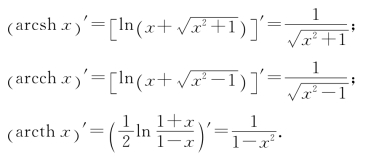
例14 设y＝ln
解 y＝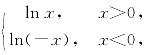
则
当x＞0时，
＝（lnx）′＝
；当x＜0时，
＝［ln（－x）］′＝
即
例15 设f（x）＝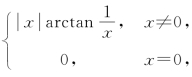
则
（1）求f′（x）；（2）讨论f′（x）在（－∞，∞）的连续性.
解 （1）因为
＝0＝f（0），所以f（x）在x＝0连续.
当x≠0时，f′（x）＝
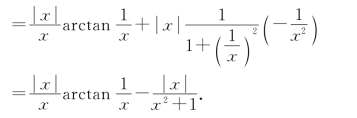
当x＝0时，
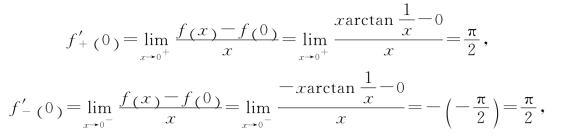
即左右导数存在且相等，所以f（x）在x＝0处可导，且f′（0）＝
.于是
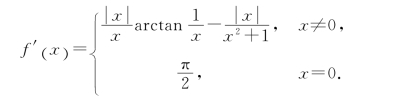
（2）现在考虑f′（x）在x＝0处的连续性.先考察其在x＝0处的左、右极限.
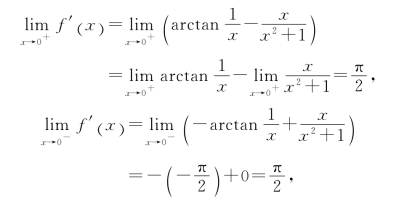
即f′（x）在x＝0处的左、右极限存在且相等，所以f′（x）在x＝0处连续.因此，f′（x）在（－∞，∞）上连续.
在讨论了初等函数的求导公式和求导法则之后，为了使用方便，归纳如下：
1.导数的基本公式
（1）（C）′＝0（C为常数）；
（2）（xα）′＝αxα－1；
（3）（ax）′＝axln a，（ex）′＝ex；
（4）（logax）′＝
，（ln x）′＝
（5）（sin x）′＝cos x；
（6）（cos x）′＝－sin x；
（7）（tanx）′＝sec2 x；
（8）（cotx）′＝－csc2 x；
（9）（secx）′＝sec xtan x；
（10）（cscx）′＝－csc xcot x；
（11）（arcsinx）′＝
（12）（arccosx）′＝
（13）（arctanx）′＝
（14）（arccotx）′＝
（15）（shx）′＝ch x，（chx）′＝sh x；
（16）（thx）′＝
，（cthx）′＝－
（17）（arcshx）′＝
，（arcchx）′＝
（18）（arcthx）′＝
2.导数的四则运算法则
设函数u＝u（x），v＝v（x）可导，则有
（1）［Cu］′＝Cu′（C为常数）；
（2）［u±v］′＝u′±v′；
（3）［uv］′＝u′v＋uv′；
（4）
3.复合函数的求导法则
设y＝f（u）关于u可导，u＝φ（x）关于x可导，则复合函数y＝f［φ（x）］关于x可导，且
