反函数的求导法则

二、反函数的求导法则

定理1 设函数y＝f（x）在点x的某邻域内连续且严格单调，且在点x可导，导函数不为零，则它的反函数x＝φ（y）在点y （y＝f（x））可导，且

证 因为函数y＝f（x）在x的某邻域内连续且严格单调，则在该邻域内存在反函数x＝φ（y），并且x＝φ（y）连续.

记Δx＝φ（y＋Δy）－φ（y）；Δy＝f （x＋Δx）－f（x）.

则当Δy→0时，Δx→0.于是

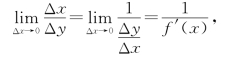
所以，x＝φ（y）在点y可导，且其导函数为

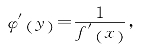
即反函数的导函数是其原函数导数的倒数.

例6 设y＝logax（a＞0，a≠1），求y′.

解 对数函数y＝logax是指数函数x＝ay的反函数，满足定理1的条件.已知（ay）′＝ayln a≠0，所以

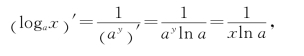
即

特别地，（lnx）′＝

例7 设y＝arcsin x，求y′.

解 因为y＝arcsin x在（－1，1）上存在反函数x＝sin y，y∈（－），且x＝sin y严格单调，导函数

（siny）′＝cos y≠0，

所以

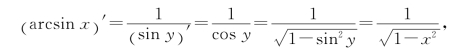
即

用同样的方法可得

例8 设y＝arctan x，求y′.

解 y＝arctan x在（－∞，∞）上存在反函数x＝tan y，y∈（－），满足定理1的条件，所以

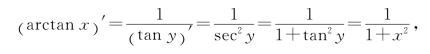
即

用同样的方法可得