五、刘维尔公式

五、刘维尔公式

定理3（刘维尔公式） 设y1（x）是方程y″＋p（x）y′＋q（x）y＝0的一个特解，则方程的另一个与y1（x）线性无关的特解为

该公式称为刘维尔公式.

证 设y2（x）＝y1（x）v（x），其中v（x）是待定函数，则有

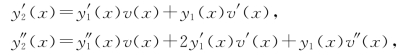
代入方程，得

y″1v＋2y′1v′＋y1v″＋p（x）（y′1v＋y1v′）＋q（x）y1v＝0，

整理得

y1v″＋［2y′1＋p（x）y1］v′＋［y″1＋p（x）y′1＋q（x）y1］v＝0.

因为y1是原方程的解，故待定函数v（x）满足方程为

y1v″＋［2y′1＋p（x）y1］v′＝0，

这是一个可降阶的二阶微分方程.

令v′＝z，则v″＝.于是

求解后得

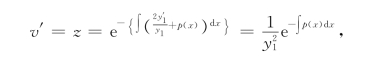
再积分后得

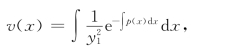
于是有

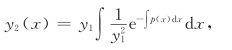
又因为＝v（x）不是常数，因而y是与y线性无关的另一个特解.21

由此定理可知，若能知道二阶齐次线性方程的一个特解，则可利用刘维尔公式求出另一个与它线性无关的特解，从而可写出该方程的通解.

例3 设有二阶线性方程x2 y″＋xy′－y＝0，试用观察法先求一个特解，再用刘维尔公式求另一个线性无关的特解.

解 由于方程的系数是x的多项式，猜想可能有多项式形式的特解.由观察知y1＝x是它的一个特解.

再由刘维尔公式将y1＝x和p（x）＝代入，得

另外，由于与－线性相关，且都满足方程，故可选一个与y＝x线性无关的简单的特解，1自然以＝y最适合.2