一、极限存在准则
极限存在准则Ⅰ（夹逼定理）
设数列｛xn｝，｛yn｝，｛zn｝满足：
（1）yn≤xn≤zn（n＝1，2，…），
（2）
yn＝
zn＝a，则极限
xn存在，且
xn＝a.
证 因为
yn＝a＝
zn，所以对∀ε＞0，∃N1，当n＞N1时，有
a－ε＜yn＜a＋ε，
对上述ε＞0，∃N2，当n＞N2时，有
a－ε＜zn＜a＋ε.
取N＝max ｛N1，N2｝，当n＞N时，有
a－ε＜yn≤xn≤zn＜a＋ε，
即
＜ε，这就证明了
xn＝a.
此定理对函数的极限仍然成立.
极限存在准则Ⅰ′ 设函数f（x），g（x），h （x）在x0的某去心邻域U（x0，δ）内满足：
（1）g（x）≤f（x）≤h （x），
（2）
g（x）＝
h （x）＝A，则有
f（x）＝A.
证略.
在上述准则中，若把x→x换成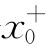x→
，x→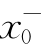
，x→∞，x→＋∞，x→－∞时，结论仍然成立.0
例1 证明
＝1 （a＞0，a≠1）.
证 设a＞1，并令λn＝
－1＞0，则有
＝1＋λn，所以
即
由于
＝0，由夹逼定理知
λn＝0.即
）－1＝0，则有
当0＜a＜1时，令b＝
＞1，则有
综上所述，
＝1成立.
极限存在准则Ⅱ 单调有界数列必有极限.即
若数列｛xn｝单调递增且有上界，即xn≤M （n＝1，2，…），则极限
xn存在，且
xn＝a≤M；
若数列｛xn｝单调递减且有下界，即xn≥L （n＝1，2，…），则极限
xn存在，且
xn＝a≥L.
图1－19
对此定理不给出严格的理论证明，只给出几何解释.以｛xn｝单调递增为例，此时在数轴上对应于数列的点xn随着n的递增向x轴正向移动，如图1－19所示.这时数列｛xn｝只有两种变化趋势，一种是当n→∞时，xn→＋∞；另一种是当n→∞时，xn以某一定数a为极限.又因为｛xn｝有上界，所以xn→＋∞是不可能的.于是有
xn＝a.
极限存在准则Ⅱ′ 若函数f（x）在开区间（a，b）上单调有界，则极限
f（x）和
f（x）存在.
例2 设x1＝
，x2＝
，…，xn＋1＝
，…，求
解 显然｛xn｝单调递增：x1＜x2＜…＜xn＜xn＋1…，
又 x1＝
设xn＜
＋1，则xn＋1＝
＋1.
由数学归纳法知，对于每一个n，xn＜
＋1成立，即数列｛xn｝有上界.根据极限存在准则Ⅱ，
xn存在.
设
xn＝a＞0，由xn＋1＝
可得
＝xn＋5.
在上式两边同时取极限，再由极限的运算法则，有
（xn＋5），可得
a2－a－5＝0.
解得
，因为a＞0，舍去负值，
故
例3 证明
cos x＝1.
证 0≤
因为
＝0，由极限存在准则Ⅰ′可得
cos x＝1.