习题6－4

习题6－4

1.求下列微分方程的解.

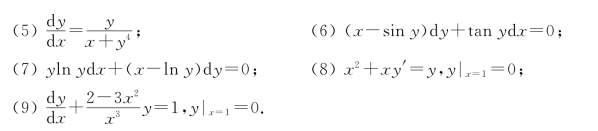
2.设曲线L位于xOy平面的第一象限内，L上任一点M处的切线与y轴总相交，交点记为A.已知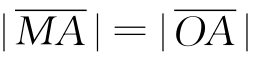，且L过点（），求L的方程.

3.用适当的变量代换将下列方程化为可分离变量的方程，然后求其通解.

（1）＝（x＋y）2； （2）xy′＋y＝y（ln x＋ln y）；

（3）y′＝y2＋2（sin x－1）y＋sin2 x－2sin x－cos x＋1.

＊4.求下列方程的解.

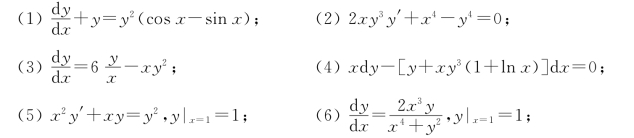
（7）（y4－3x2）dy＋xydx＝0.

5.设函数f（x）可导，且对任何x，y有f（x＋y）＝eyf（x）＋exf（y），f′（0）＝e，求函数f（x）.

6.设＋φ′（x）y＝φ（x）φ′（x），其中φ（x）为已知函数，求y（x）.

7.一质量为m的物体作直线运动，从速度等于零的时刻起，有一个与运动方向一致、大小与时间成正比（比例系数为k1）的力作用于它，同时还受到一个与速度成正比（比例系数为k2）的阻力作用，求物体运动的速度与时间的关系.

8.设y＝ex是微分方程xy′＋p（x）y＝x的一个解，求此微分方程满足条件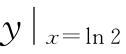＝0的特解.