三、最值
根据闭区间上连续函数的性质，若函数f（x）在［a，b］上连续，则f（x）在［a，b］上一定存在最大值与最小值.而函数在开区间（a，b）内的最值点必为极值点，从而通过比较（a，b）内的不可导点、驻点及区间端点a，b的函数值，从中找到f（x）在［a，b］上的最大最小值.下面举例说明最值的求解过程.
例5 求f（x）＝｜2x3－9x2＋12x｜在
上的最大值与最小值.
解 因为
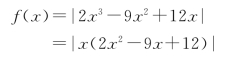
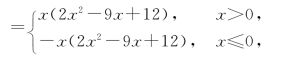
所以
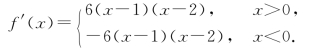
由f′＋（0）及f′－（0）的定义可求得f′＋（0）＝12，f′－（0）＝－12，因此函数在x＝0不可导.
在（0，
）内有驻点x＝1，x＝2.比较它们与端点－
和
的函数值：
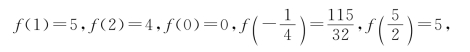
故f（x）在x＝1和x＝
处取得最大值5，在x＝0处取得最小值0.
不难理解，若f（x）在区间I上连续，且存在唯一的极值点x0，则x0必为最值点，即若x0为极大（小）值点，则x0必为I上的最大（小）值点.有兴趣的读者可自行证明.
在实际问题中，若f（x）在某区间上存在最值，且在区间内部求得唯一一个可能的极值点，则不需要作任何判断便可肯定此点为所求最值点.
例6 要建造一个体积为50m3的有盖圆柱形水池，问水池的高和底面半径取多大时用料最省？
解 用料是指水池的表面积.
设水池底面半径为r.高为h，则它的表面积为
S＝2πr2＋2πrh.
由于体积V＝50＝πr2 h，即h＝
，代入上式得到S为r的函数，即
下面讨论函数S（r）在r取何值时有最小值.
因为
求得唯一驻点
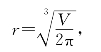
而且这个实际问题确实存在最小表面积，所以当r＝
时，S最小.此时高为
将V＝50代入上式得h＝2
≈4m.
这说明当底面直径与水池的高相等时用料最省.
例7 一艘轮船在航行中的燃料费和它的速度的立方成正比.已知当速度为10km／h时，燃料费为每小时6元，而其他与速度无关的费用为每小时96元.问轮船的速度为多少时，每航行1km所耗的费用最小？
解 设船速为xkm／h，则所耗的燃料费为y＝kx3.
由已知当x＝10时，y＝6，从而求得比例系数k＝0.006.根据题意，轮船每航行1km所耗的费用为
下面，问题转化为求f（x）的最小值.
由于
求得驻点x＝20.
当x＜20时，f′（x）＜0；x＞20时f′（x）＞0.根据极值的第一充分条件，x＝20为f（x）的唯一极小值点，因而必为最小值点，且最小值为0.006×202＋
＝7.2元.
因此，当船速为20km／h时，每航行1km的耗费最小，且耗费为7.2元.