一、函数的单调性
观察处处可导的单调递增函数的切线与单调递减函数的切线时可发现，增函数各点处的切线与x轴正向的夹角为锐角，从而知导函数非负；减函数各点处的切线与x轴正向的夹角为钝角，从而知导函数非正，如图3－8所示.因此，有如下定理.
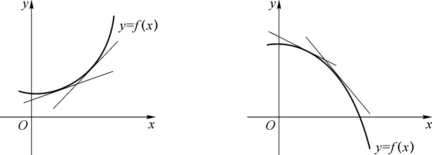
图3－8
定理1 设f（x）在区间I上可导，则f（x）在I上递增（减）的充要条件为
f′（x）≥0 （f′（x）≤0）.
证 （必要性）设f（x）在I上为增函数，则对任何x0∈I，当x≠x0，x∈I时有
令x→x0，便得f′（x0）≥0.
（充分性）若f（x）在区间I上恒有f′（x）≥0，则对任何x1，x2∈I（x1＜x2），应用拉格朗日中值定理，存在ξ∈（x1，x2），使得
f（x2）－f（x1）＝f′（ξ）（x2－x1）≥0，
即
f（x1）≤f（x2），
由此便知f（x）在I上为增函数.
对减函数的情形可以类似证明.
在上述定理充分性的证明中，若定理条件改为f′（x）＞0，易知f（x）在I上为严格增函数，但反之不成立.例如，f（x）＝x3，显然f（x）在（－∞，＋∞）严格单调递增，但在（－∞，＋∞）上并非恒有f′（x）＞0（f′（0）＝0）.从而有以下推论及定理.
推论1 设f（x）在区间I上可导，且在区间I上恒有
f′ （x）＞0 （f′（x）＜0），
则f（x）在区间I上严格单调递增（减）.
定理2 设函数f（x）在区间（a，b）内可导，则f（x）在（a，b）内严格递增（递减）的充要条件是：
（1）对一切x∈（a，b），有f′（x）≥0（f′（x）≤0）；
（2）在（a，b）内的任何子区间上f′（x）≢0.
证 只证单调递增的情况，单调递减的情形可类似证明.
（必要性）设f（x）在（a，b）上严格递增，由前面定理知（1）成立.下面用反证法证明（2）.
若存在（a，b）的子区间（a1，b1），f（x）在（a1，b1）上满足f′（x）＝0，则f（x）在（a1，b1）上为常数.这与f（x）在（a，b）上严格递增矛盾.
（充分性）若f（x）满足条件（1）、（2）.首先由条件（1）知，f（x）为（a，b）上的增函数.下面用反证法证明f（x）严格递增.
假设f（x）在（a，b）上不为严格递增函数，则存在x1，x2∈（a，b），x1＜x2，使得
f（x1）＝f（x2）.
由于f（x）在（a，b）上为增函数，则对于任何x∈（x1，x2），有
f（x1）≤f（x）≤f（x2），
从而有
f（x1）＝f（x）＝f（x2），
这说明f（x）在子区间（x1，x2）上为常数，与条件（2）矛盾.
注意 若函数f（x）在端点a右连续，在（a，b）内可导，则以上定理的条件（1）、（2）为f（x）在区间［a，b）严格单调的充要条件.对于函数f（x）在端点b左连续或同时在端点a，b上连续的情形可类似讨论.
例1 设f（x）＝3x－x3.试讨论函数f（x）的单调区间.
解 因f′（x）＝3－3x2＝3（1＋x）（1－x）.因而，在（－1，1）内，f′（x）＞0，函数f（x）严格单调递增；在（－∞，－1）与（1，＋∞）内，f′（x）＜0，函数f（x）严格单调递减.对f（x）＝3x－x3的单调区间列表如下（表中
表示递增
表示递减）.
例2 证明不等式sin x＞x－
（x＞0）.
分析：需证明sin x－x＋
＞0.为此，考虑函数f（x）＝sin x－x＋
.由于f（0）＝0，要证f（x）＞0＝f（0），只需证f（x）在［0，＋∞）上严格单调递增即可，从而考虑是否有f′（x）＞0.f′（x）＝cos x－1＋
现在需证明f′（x）＝cos x－1＋
＞0.由于f′（0）＝0.需证f′（x）＞f′（0）（x＞0），因而类似以上分析，考虑是否有f″（x）＞0.此时，由于x＞0时，sin x＜x.从而有f″（x）＝－sin x＋x＞0.下面给出证明过程.
证 设f（x）＝sin x－x＋
，则
由于x＞0时，sin x＜x.所以有
f″（x）＞0 （x＞0），
这说明f′（x）在［0，＋∞）上严格单调递增，从而有
这同样说明f（x）在［0，＋∞）上严格单调递增，从而又有
即证得不等式
例3 证明对每个自然数n，方程xn＋2－2xn－1＝0只有唯一正根.
证 设f（x）＝xn＋2－2xn－1.
由于f（0）＝－1，
f（x）＝＋∞.利用连续函数的介值性可知，f（x）＝0有正根.为了证明正根的唯一性，先考察f（x）的单调性.将其求导得
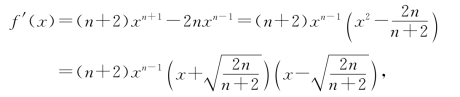
因此，f（x）在［0，＋∞）上点x0＝处导数为0.在（0，x0）内f′（x）＜0，f（x）严格递减；在（x0，＋∞）内f′（x）＞0，f（x）严格递增，结合f（0）＝－1，可知f（x）除在（x0，＋∞）内有唯一正根外设有其他正根.