定积分的换元法与分部积分法
由牛顿－莱布尼茨公式可知，可用求不定积分的方法求定积分，从而可将不定积分的换元法和分部积分法移植到定积分的计算中.
定理3（定积分的换元法） 若函数f（x）在［a，b］上连续，x＝φ（t）在［α，β］上有连续的导函数，且φ（α）＝a，φ（β）＝b，a≤φ（t）≤b，t∈［α，β］，则有定积分的换元公式：
证 易知式（2）两边的被积函数均连续，从而均有原函数.设F（x）为f（x）在［a，b］上的一个原函数，由复合函数求导法可知
即F［φ（t）］为f［φ（t）］φ′（t）的一个原函数.
从而由牛顿－莱布尼茨公式
应用式（2）时要注意，将积分变量由x换为t后，积分限也要换为新变量t的对应取值.但在求出f［φ（t）］φ′（t）的原函数之后，直接将变量t的积分上下限代入这个原函数并求其差即可，不必再还原回变量x.这是定积分换元法与不定积分换元法的区别，这一区别的原因是在于定积分为一个数，如果式（2）右边可以计算出此数，则左边也就被计算出.而不定积分求原函数，应当保留原变量.
例6 求
解 设x＝2sint，（｜t｜＜
），则x＝0时，t＝0；x＝1时，t＝
.因此
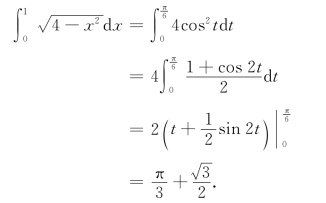
例7 求
解 设sin x＝u，当x＝0时，u＝0；当x＝
时，u＝1.
则
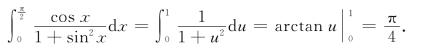
为了方便起见，以上过程可写为
此时，没有引入新变量u，自变量仍为x，虽然在凑微分的过程中的已将sin x视为整体，但只要不引入新变量，积分上下限就不必改变.
例8 证明：
（1）若f（x）为［－a，a］上连续的偶函数，则
（2）若f（x）为［－a，a］上连续的奇函数，则
（3）若f（x）为（－∞，＋∞）上连续的周期函数，周期为T，则
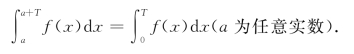
证 （1）由于f（x）为偶函数，则f（－x）＝f（x）.那么
对于右边第一式，利用代换x＝－t，则
从而有
（2）参照例8（1）即可证明.
（3）（方法一）由积分区间的可加性得
对右边第三式利用变换x＝T＋t，则
从而有
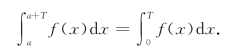
（方法二）可视
为变限积分.设F（a）＝
f（x）dx，a∈（－∞，＋∞），则
F′（a）＝f（a＋T）－f（a）＝0，
从而得F（a）为常数，则
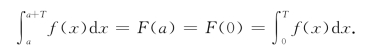
定理4（定积分的分部积分法） 设u（x）和v（x）均在［a，b］上有连续导函数，则
证 由于u（x）v（x）为u′（x）v（x）＋u（x）v′（x）的一个原函数，则
从而得
例9 求I＝sec3 xdx.
解
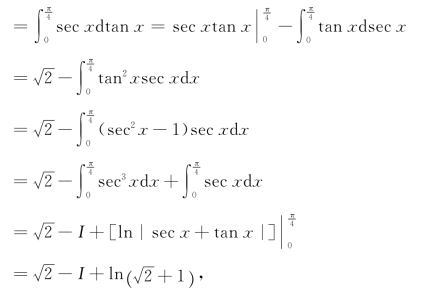
从而有
所以
例10 计算定积分In＝
sinnxdx和Jn＝
cosnxdx（n＝1，2，…）.
解
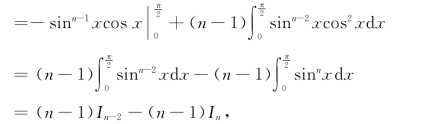
从而有递推公式
由于易计算出
所以，反复利用递推公式，有
令x＝
－t，可得
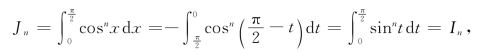
因而这两个积分相等.