二、两个重要极限

二、两个重要极限

作为极限存在准则的应用，下面来证明两个重要极限.

重要极限1

证 先证时的情形.作单位圆（如图1－20所示），设圆心角∠AOB＝x

考虑0＜x＜，在A点画圆的切线AD与OB延长线交于D，使BC⊥OA并与OA相交于C，则sin x＝BC，tan x＝AD.

因为

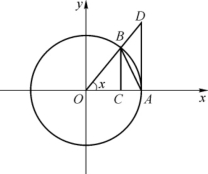
图1－20

△AOB的面积＜扇形AOB的面积＜△AOD的面积，得

即

又

由夹逼定理可得

即

由于是偶函数，所以

综上得

例4 求

解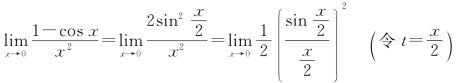

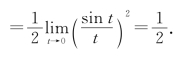
例5 求（1－x ）tan

解 令t＝1－x，则x→1时，t→0.所以

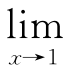（1－x ）tan

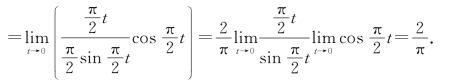
重要极限2＝e.

证 （1）先证xn＝单调递增.

利用不等式“几何平均值小于算术平均值”，有

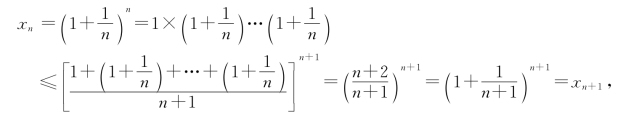
即｛xn｝单调递增.

（2）再证｛xn｝有上界.

根据二项式展开定理，有

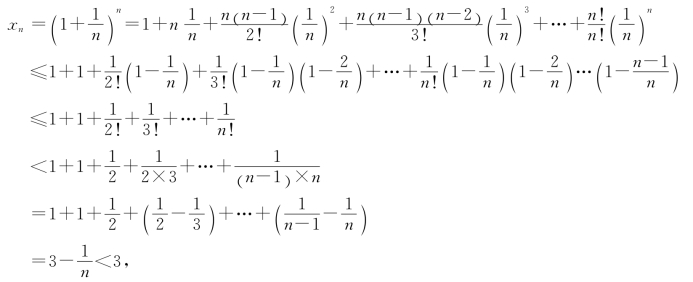
所以｛xn｝有上界3.

根据极限存在准则Ⅱ知，存在记其极限为

其中，e＝2.718 281 828 459….

例6 证明

证 （1）先考虑x→＋∞的情形.

对充分大的整数x，总存在自然数n，使得n≤x＜n＋1.此时

有

从而

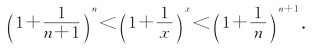
因为

由夹逼定理知

（2）再证x→－∞的情形.

令t＝－（x＋1），则当x→－∞时t→＋∞，所以

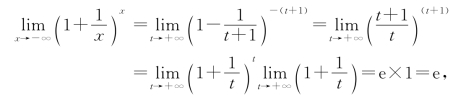
即

若令u＝，当x→0时u→∞，所以

例7 求

解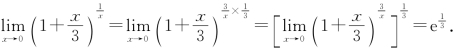

例8 求

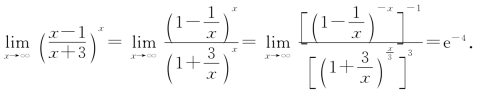
解