由参数方程所确定的函数求导法

二、由参数方程所确定的函数求导法

参数方程

在平面上表示一条椭圆曲线，消去参数t可以得到y与x的关系式

一般而言，参数方程

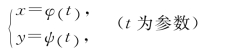
表示平面上的一条曲线.如果能从这个方程组中消去参数t，则可以得到y与x的函数关系，它要么是显函数，要么是隐函数，这样可以用前面所学的方法求出y对x的导数.但是，多数情况下很难消去参数t，此时又怎样求呢？

设x＝φ（t）存在单值反函数t＝φ－1（x），且满足反函数求导的条件，于是y可看作复合函数

y＝ψ［φ－1（x）］，

利用复合函数和反函数的求导法则，有

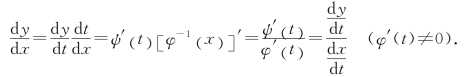
类似地，y关于x的二阶导数

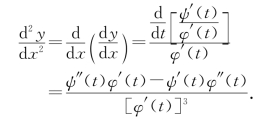
例7 求摆线

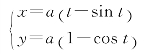
在t＝，t＝π处的切线方程.

解 由于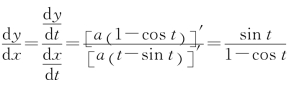，则

当t＝时，对应摆线上点（a（－1），a）的切线斜率

所以，t＝时摆线的切线方程为

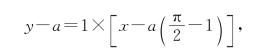
即

当t＝π时，对应摆线上点（aπ，2a）的切线斜率

所以，t＝π时摆线的切线方程为

y＝2a.

例8 设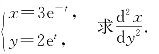

解 此参数方程确定的函数关系为x＝x（y），根据参数方程求导法，得

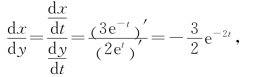
再对y求导，得

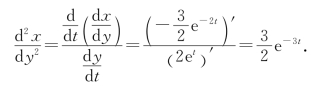
例9 求对数螺线r＝eaθ在θ＝处的切线方程.

解 把极坐标方程化成参数方程，有

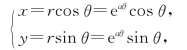
所以

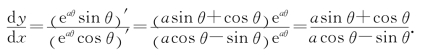
当θ＝时，曲线上点（0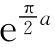，）处的切线斜率为

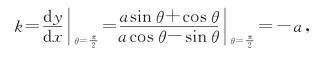
于是，所求切线方程为

即