带有拉格朗日型余项的泰勒公式
前面所讲的带有佩亚诺型余项的泰勒公式只是定性地说明：当x→x0时用n次多项式逼近函数f（x）的误差是较（x－x0）n高阶的无穷小量.下面将构造一个定量形式的余项，以便于对误差进行计算或估计.
泰勒定理 若函数f（x）在［a，b］上存在直至n阶连续导函数，在（a，b）内存在n＋1阶导数，则对于任意给定的x，x0∈［a，b］至少存在一点ξ∈（a，b），使得
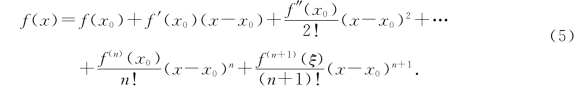
证 作辅助函数
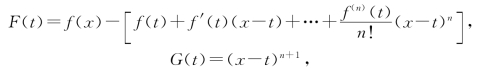
所需证的式（5）即为
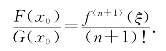
不妨设x0＜x，由于
则F（x）与G（x）在［x0，x］上满足柯西中值定理条件，注意到F（x）＝G（x）＝0，从而存在ξ∈（x0，x）⊂（a，b），使
式（5）同样称为泰勒公式，它的余项
称为拉格朗日型余项，其中ξ可写为ξ＝x0＋θ（x－x0）（0＜θ＜1），所以式（5）又称为带有拉格朗日型余项的泰勒公式.
当n＝0时，式（5）即为拉格朗日中值公式，即
f（x）－f（x0）＝f′（ξ）（x－x0），
所以，泰勒定理为拉格朗日中值定理的推广形式.
当x0＝0时，得到如下的泰勒公式
式（6）也称为（带有拉格朗日型余项的）麦克劳林公式.
例5 写出例1中六个函数的带有拉格朗日型余项的麦克劳林公式.
解 先写出六个公式，随后验证其中两个.
（1）ex＝1＋x＋
＋…＋
， 0＜θ＜1，x∈（－∞，＋∞）.
（2）sin x＝x－
＋…＋（－1）m－1
（3）cos x＝1－
＋…＋（－1）m
（4）ln（1＋x）＝x－
＋…＋（－1）n－1
（5）（1＋x）α＝1＋αx＋
x2＋…＋
（6）＝1＋x＋x2＋…＋xn＋
，0＜θ＜1，｜x｜＜1.
下面只验证（1）和（2），其余留给读者自行验证.
（1）设f（x）＝ex.
因为
f′（x）＝f″（x）＝…＝f（n）（x）＝ex，
所以
f（0）＝f′（0）＝f″（0）＝…＝f（n）（0）＝1.
又由于
将以上所得代入式（6），便得ex的麦克劳林公式.
由这个公式可知，若用ex的n次泰勒多项式近似表示ex，即
所产生的误差为
如果取x＝1，无理数e可近似写为
误差为
容易计算出，n＝10时，e≈2.718 282，误差不超过10－8.
（2）设f（x）＝sin x.
因为
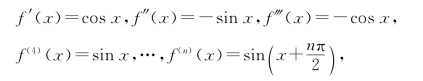
所以
f（0）＝0，f′（0）＝1，f″（0）＝0，f‴（0）＝－1，f（4）（0）＝0，…（循环取0，1，0，－1四个数）.
令n＝2m，并注意到
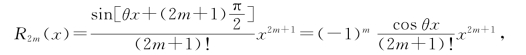
将以上所得代入式（6），便得到sin x的麦克劳林公式.
如果取m＝1，2，3，代入sin x的麦克劳林公式，可得近似式
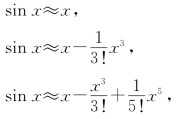
其误差的绝对值依次不超过
读者可从图3－7中比较正弦函数与以上三个泰勒多项式的图像.
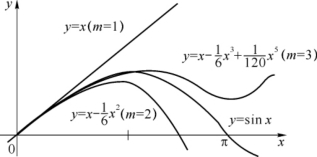
图3－7
例6 证明e为无理数.
证 由ex的麦克劳林公式（例5（1）），当x＝1时有
从而可得
若e为有理数（设为
，p和q为正整数），则当n＞p时，n！e为正整数，从而上式左端为整数.由于
，故当n≥2时右端为非整数，得出矛盾.故e必为无理数.