y″＝f（x，y′）型的微分方程

二、y″＝f（x，y′）型的微分方程

方程

的右端不显含未知函数y.

做变量替换，令y′＝p（x），则y″＝p′（x），代入原方程中，则

p′＝f（x，p）

是关于x，p的一阶微分方程，若其通解为p＝φ（x，C1），则原方程化为

对其两端积分，便得方程（7）的通解为y＝∫φ（x，C1）dx＋C2，其中C1，C2为任意常数.

例3 悬链线方程的结果是历史上一个著名的力学问题，该问题最初由詹姆斯·伯努利在1690年提出.在此之前，伽利略曾关注过该问题，并猜想这条曲线是抛物线，惠更斯曾利用几何方法证明它不是抛物线，最后，约翰·伯努利解决了这个问题.莱布尼兹将其命名为悬链线，在工程中有广泛应用.设有一质量均匀、柔软且不能伸缩的绳索，两端分别被固定在两个不同的位置，它在重力作用下处于平衡状态.试求绳索在平衡状态时所对应的曲线方程.

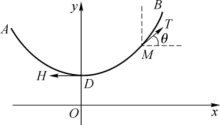
图6－2

解 取坐标系，如图6－2所示.

设绳索最低点为D，取y轴通过点D铅直向上，x轴水平向右，且点D到原点O的距离为一定值a0（a0≠0），待定.

由题意，曲线在D点处切线斜率为零.设M（x，y）为绳索上任一点，的弧长为s，绳索的线密度为ρ，分析的受力情况.因为绳索是柔软的，所以没有弯曲的反抗力，在两端固定的情况下，只受张力的作用.设点D处的水平张力为常数H，在点M（x，y）处切向张力的大小为T，它与x轴夹角为θ.

把作用于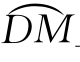上的力沿水平和垂直两个方向分解，由静力平衡条件得

Tcosθ＝H， Tsinθ＝ρgs，

于是有

又y′＝tanθ且s＝dx，代入上式，求导整理得

其中a＝.且满足初始条件

方程（8）不显含y，因而可令y′＝p（x），则y″＝p′（x），代入方程（8）得

变量分离后得

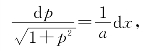
两边积分，有

即

把初始条件y′（0）＝0代入，有p（0）＝0，得C1＝0.

于是，arcshp＝，即p＝sh

再由p＝y′，得y′＝sh，两边积分后得

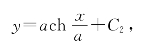
再由y（0）＝a0，得C2＝a0－a.

于是，悬链线方程为

若令待定常数a0＝a，也即事先选坐标系时，使绳索最低点D与x轴距离为a＝，则所求悬链线表达式为y＝ach

众所周知，当｜x｜很小时，由于chx2＋o（x2），故悬链线y＝ach近似于抛物线y＝a＋.因此，伽利略猜想悬链线为抛物线还是比较接近的.

例4 解方程y″－y′＝2ex.

解 方程两边不显含未知函数y，故可令y′＝p（x），则y″＝p′（x）.因此，原方程化为

p′－p＝2ex，

这是一个关于x和p的一阶线性微分方程，解得

上式两端积分，得

其中C1、C2为任意常数.