无穷小量的性质

二、无穷小量的性质

为叙述方便，下面的定理中只证明x→x0的情形.定理结论对自变量的其他趋向同样成立.

定理3 有限个无穷小量的和仍为无穷小量.

证 只考虑两个无穷小量的情形.设 α（x）＝0β（x）＝0，即：

对∀ε＞0，∃δ1＞0，当0＜＜δ1时，有

对上述ε＞0，∃δ2＞0，当0＜＜δ2时，有

取δ＝min｛δ1，δ2｝，则当0＜＜δ时，

即

注意 无穷多个无穷小量的和未必是无穷小量，如＝0，但是

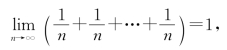
此处无穷多个无穷小量的和却等于1.

定理4 有界变量与无穷小量的乘积仍为无穷小量.

证 设f（x）在某个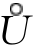 （x0，δ0）中有界，即当x∈ 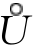（x0，δ0）时，＜M；又

故对∀ε＞0，∃δ1＞0，当0＜＜δ1时有

取δ＝min｛δ0，δ1｝，则当0＜＜δ时，

即

例5 证明＝0.

证 因为≤1，由定理4知，原极限为零.

推论1 常数与无穷小量的乘积仍为无穷小量.

推论2 有限个无穷小量的乘积仍为无穷小量.