三、函数作图

三、函数作图

前面利用导数讨论了函数的单调性、极值与凸凹性，并研究了曲线的渐近线.根据这些知识可以画出函数的图像，这对直观把握函数的性质有很大的帮助.

作图的步骤大致可概括为如下几步：

（1）确定函数y＝f（x）的定义域，讨论一些基本性质，如奇偶性、对称性和周期性及与坐标轴的交点；

（2）求出使f′（x）＝0，f″（x）＝0及f′（x），f″（x）不存在的点；

（3）确定函数的单调区间、凸凹区间、极值点、拐点；

（4）求渐近线；

（5）描点作图.

例3 作曲线y＝＋1（x＞0）的图形.

解 （1）函数的定义域为（0，＋∞），与x轴交点为（1，0）.

（2）由y′＝＝0，得x＝1；由y″＝＝0，得x＝

（3）列表讨论单调区间与凸凹区间.

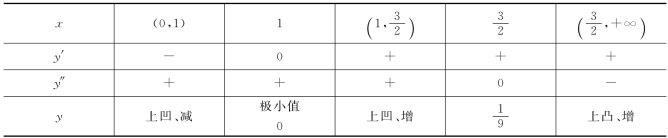
由表可知，（）为曲线的拐点.

（4）讨论曲线的渐近线.

由（＋1）＝∞，知x＝0为曲线的垂直渐近线；

由（＋1）＝1，知y＝1为曲线的水平渐近线.

（5）作图（见图3－14）.

例4 作函数y＝的图形.

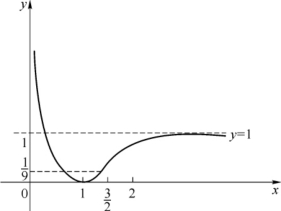
图3－14

解 （1）函数定义域为（－∞，－1）∪（－1，＋∞），与x轴交点为（0，0）.

（2）由y′＝＝0，得x＝0，x＝－2；当x＝－1时y′不存在.由y″＝知，当x＝－1时，y″不存在.

（3）列表讨论单调区间与凸凹区间.

（4）求曲线的渐近线.

由＝∞，知x＝－1为垂直渐近线；

由k＝＝1，b＝［f（x）－kx］＝＝－1，知y＝x－

1为斜渐近线.

（5）作图（见图3－15）.

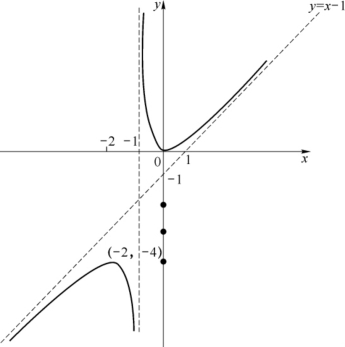
图3－15