y（n）＝f（x）型的微分方程

一、y （n）＝f（x）型的微分方程

方程

的右端仅含有自变量x.易知，（1）式可看作y（n－1）为未知函数的一阶微分方程，两边积分得

类似地，上式可视为y（n－2）为未知函数的一阶微分方程，再积分得

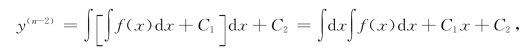
依此法，经n次积分后得

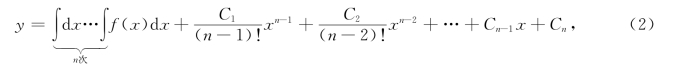
其中C1，C2，…，Cn为任意常数，（2）式为方程（1）的通解.

例1 解方程y‴＝xex.

解 对所给方程接连积分三次得

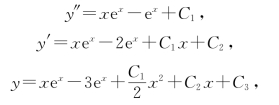
为所求方程通解，其中C1，C2，C3为任意常数.

例2 质量为m的质点受力F的作用，沿x轴作直线运动，设力F只与时间t有关，并设当t＝0时，F（0）＝1，力F随时间的增大均匀地减小，直到t＝T时，F（T）＝0.如果开始时质点位于原点，且初速度为零，求这质点的运动规律.

解 设t时刻质点的位置函数为x＝x（t）.由牛顿第二定律知

由已知条件，可令F（t）＝kt＋b且F（0）＝1，F（T）＝0，得k＝－，b＝1即F（t）＝1－.于是，方程（3）可化为

且满足

将方程（4）连续积分两次，得

把（5）式和（6）式代入上式，得C1＝0，C2＝0.

故质点的运动规律为