六、常数变易法
对于一般的二阶非齐次线性方程而言，在求出对应齐次方程的两个线性无关的特解后，也可用常数变易法求得非齐次方程的特解y＊.
下面以二阶线性微分方程为例讨论高阶线性方程的常数变易法.
设y1（x）和y2（x）是二阶齐次线性微分方程
的两个线性无关的解，现来求非齐次线性微分方程
的通解.
由前面分析知方程（5）的通解可写为
Y（x）＝C1y1（x）＋C2y2（x）.
设方程（6）的通解形式为
下面确定未知函数C1（x）及C2（x）.为方便起见，用C1，C2分别代替C1（x），C2（x）.
对（7）式两端求导，得
y′（x）＝y′1（x）C1＋y1（x）C′1＋y′2（x）C2＋y2（x）C′2.
由于两个未知函数C1（x）和C2（x）只需满足方程（6），可以规定它们再满足一个关系式.为简便起见，由y′表达式可知，为了使y″表达式中不含C″1和C″2，可设
则
y′＝y′1C1＋y′2C2，
两边再求导，得
y″＝y′1C′1＋y″1C1＋y′2C′2＋y″2C2.
把y，y′和y″表达式代入方程（6），得
y′1C′1＋y′2C′2＋（y″1＋py′1＋qy1）C1＋（y″2＋py′2＋qy2）C2＝f，
整理并注意到y1和y2是齐次方程（5）的解，故上式即为
联立式（8）和（9），在系数行列式
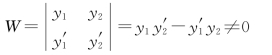
时可解得
对上式两端积分（假定f（x）连续），得
于是得非齐次方程（6）的通解为
其中D1和D2为任意常数.
例4 已知方程（1－x）y″＋xy′－y＝1所对应的齐次方程的两个解为x和ex，求方程的通解.
解 由于
≠常数，故x和ex为方程的两个线性无关的解.
令y＝C1（x）x＋C2（x）ex为其通解，则
y′＝xC′1（x）＋exC′2（x）＋C1（x）＋C2（x）ex.
补充条件
于是
y′＝C1（x）＋C2（x）ex， y″＝C′1（x）＋C′2（x）ex＋C2（x）ex，
代入原方程，整理得
把（10）式和（11）式联立，解得
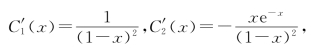
积分得
故原方程的通解为
