总习题一

总习题一

1.填空题

（1）已知f （sin ）＝cosx＋1，则f （cos ）＝________.

（2）设f（x）＝，x≠0，x≠1，则f（f（x））＝______.

（3）已知函数，则f（x）的定义域为________.

（4）设函数f（x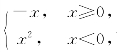）＝则g（x）＝f［f（x）］＝______；g（x）的反函数为______.

（5）设x＞0，则＝________.

（6）设f（x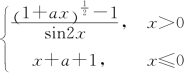）＝在x＝0连续，则a＝________.

（7）x＝π是函数f（x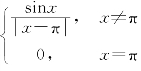）＝的________间断点（可去、跳跃或第二类）.

2.选择题

（1）设f（x）、g（x）在（－∞，∞）都是奇函数，则g［f（x）］和f［g（x）］（　）.

（A）都是偶函数　（B）都是奇函数

（C）一个是奇函数一个是偶函数　（D）都是非奇非偶函数

（2）若f（x）存在，则下列极限一定存在的是（　）.

（3）下列命题中正确的是（　）.

（A）若f（x）≥g（x），则∃δ＞0，当0＜＜δ时f（x）≥g（x）

（B）若∃δ＞0，使得当0＜＜δ时有f（x）＞g（x），且f（x）＝Ag （x）＝B都存在，则A≥B

（C）若∃δ＞0，当0＜＜δ时f（x）＞g（x），则g（x）

（D）若f（x）≥g（x），则∃δ＞0，当0＜＜δ时有f（x）＞g（x）

（4）设xn≤zn≤yn，且（yn－xn）＝0，则zn（　）.

（A）存在且等于零　（B）存在但不一定等于零

（C）不一定存在　（D）一定不存在

（5）设f（x）在点x0连续，且在x0的某空心邻域中有f（x）＞0，则（　）.

（A）f （x0）＞0　（B）f （x0）≥0

（C）f （x0）＜0　（D）f （x0）＝0

3.设函数f（x）在（－∞，∞）上是奇函数，且f（1）＝a，又对任何x均有f（x＋2）－f（x）＝f（2）.（1）试用a表示f（2）和f（5）；（2）a取何值时，f（x）是以2为周期的周期函数？

4.用极限的定义证明.

5.设对于n＝0，1，…均有0＜xn＜1，且＝－＋2xn，求xn.

6.当x→0时，下列函数分别是x的几阶无穷小量？

7.求下列极限.

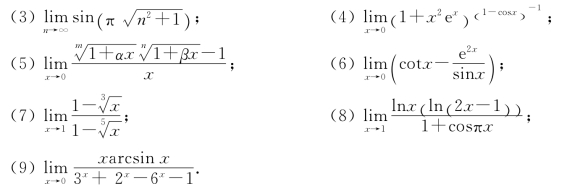
8.求函数f（x）＝（1＋x）在区间，内的间断点并判断其类型（02π）.

9.试确定a，b的值，使f（x）＝有无穷间断点x＝0和可去间断点x＝1.

10.众所周知，三条腿的椅子总能稳定着地，4条腿的椅子在起伏不平的地面上是否也能平稳地四脚着地呢？证明你的结论.