一、函数的连续性
定义1 设函数f（x）在点x0的某邻域内有定义，且满足
则称函数f（x）在点x0连续，称x0是函数f（x）的连续点.
用极限的ε－δ语言叙述：
函数f（x）在点x0连续，即对∀ε＞0，∃δ＞0，当
＜δ时有
记Δx＝x－x0，称为自变量x的改变量（或增量），则
Δy＝f（x）－f （x0）＝f （x0＋Δx）－f （x0）
称为函数y＝f（x）的改变量.此时，函数f（x）在点x0连续可定义为
即自变量的改变量趋于零时，函数的改变量也相应地趋于零.
例1 证明f（x）＝sin x在（－∞，＋∞）的任何点上连续.
证 对任意点x0∈（－∞，＋∞），当自变量x的改变量为Δx时，函数的改变量
因为
所以
由夹逼定理知
因此，f（x）＝sin x在（－∞，＋∞）的任何点上连续.
下面定义函数的左连续及右连续的概念.
定义2 若
f（x）＝f（x0），则称f（x）在点x0左连续；若
f（x）＝f（x0），则称f（x）在点x0右连续.
显然，f（x）在点x0连续的充分必要条件是:
f（x）＝f（x0）.
定义3 若函数f（x）在开区间（a，b）内每一点都连续，则称f（x）在（a，b）上连续；若f（x）在（a，b）上连续，且在点a右连续，在点b左连续，则称f（x）在闭区间［a，b］上连续.
例2 讨论函数
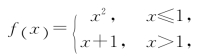
在x＝1处的连续性.
解 f（x）在x＝1有定义，且f（1）＝1.考虑f（x）在x＝1的左、右极限，
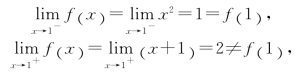
所以，f（x）在x＝1左连续，但不是右连续.因而f（x）在x＝1不连续.
例3 设f（x）在点x0连续，且f （x0）＞0，证明存在x0的某邻域，使得在此邻域内有f（x）＞
＞0.
证 因为f（x）在点x0连续，所以对∀ε＞0，∃δ＞0，当
＜δ时，有
即
f （x0）－ε＜f（x）＜f （x0）＋ε.
取ε0＝
＞0，∃δ0＞0，当
＜δ时，0
结论成立.
根据连续函数的定义，可以证明基本初等函数在其定义域内连续.