＊三、可积的必要条件与可积函数类
目前还不知何种函数可积何种函数不可积.函数的可积性是函数的又一分析性质，一些专业的“数学分析”教材中对可积理论都有较详细的讲解.至于可积函数类的问题，则需要深刻的分析学知识，在更广义的积分学理论下才能讨论清楚.为了便于后续学习，在尽可能让读者理解的情况下对这一理论的某些结论作一简单介绍.
在定积分的定义中提到，若积分和的极限存在，且不依赖于所用的分割和介点集的取法，函数便可积.换言之，无论怎么分割，无论介点集｛ξi｝如何选取，只要分割细度λ→0，积分和的极限
总存在，函数才可积，从而容易证明以下函数在定义区间上不可积.
例5 证明狄利克雷函数
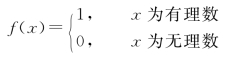
在区间［0，1］上不可积.
证 任给［0，1］一个分割
0＝x0＜x1＜x2＜…＜xn－1＜xn＝1.
由有理数集和无理数集在实数集中的稠密性，在每个小区间［xi－1，xi］上既有有理数，又有无理数.
若介点集｛ξi｝全取有理数时，积分和
若介点集｛ξi｝全取无理数时，积分和
所以，当分割细度趋于0时，以上两个积分和极限为1和0，这说明只要介点集的取法不同，积分和就有不同的极限.这便证明了f（x）在［0，1］上不可积.
例6 证明闭区间［a，b］上定义的无界函数f（x）不可积.
证 任给区间［a，b］一个分割
a＝x0＜x1＜x2＜…＜xn－1＜xn＝b，
则f（x）必在某个小区间（不妨设为第k个小区间［xk－1，xk］）上无界.
如果对任意大的函数M，总可选择一个介点集｛ξi｝，使积分和
＞M，则说明积分和的极限不存在，因此f（x）在［a，b］上不可积.
事实上，先在i≠k的各个小区间上取定介点集｛ξi｝并记G＝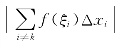
.由于f（x）在［xk－1，xk］上无界，故再取ξk∈［xk－1，xk］，使得
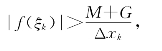
从而有
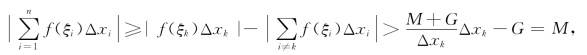
这便证明了f（x）在［a，b］上不可积.
实际上，例2证明了可积的必要条件，即可积函数必为有界函数.
定理1 若函数f（x）在［a，b］上可积，则f（x）必在［a，b］上有界.
下面列出常见的可积函数类（证明从略），但并非穷举了所有的可积函数.
（1）若f（x）为闭区间［a，b］上的连续函数，则f（x）在［a，b］上可积；
（2）若f（x）为闭区间［a，b］上只有有限个间断点的有界函数，则f（x）在［a，b］上可积；
（3）若f（x）为闭区间［a，b］上的单调函数，则f（x）在［a，b］上可积.
例7 证明函数
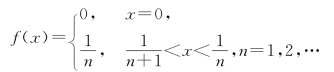
在区间［0，1］上可积（见图5－8）.
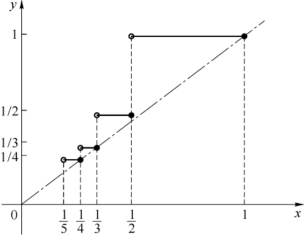
图5－8
证 此函数属以上所列的第三类函数，虽然有无穷个间断点，但由于是单调函数，因此可积.