总习题三
1.（1）
（x－2）3； （2）
； （3）f（x）＝x＋x2＋
（0＜θ＜1）；
（4）
； （5）f（e2）＝
，f（1）＝0； （6）
，－1； （7）
； （8）
2.（1）D；（2）B；（3）B；（4）C；（5）B.
3.
4.令f（x）＝ln（1＋x2），g（x）＝arctan x，在［x，1］上利用柯西中值定理.
5.（1）令F（x）＝f（x）－x，则F （
）＞0，F（1）＜0，利用介值定理；
（2）令F（x）－（f（x）－x）e－λx，F（0）＝0，又由（1）F（η）＝0，利用罗尔定理.
6.设x1，x2为f（x）的两根，x1＜x2.对F（x）＝f（x）／eax在［x1，x2］上利用罗尔定理.
7.f（x）＝f（0）＋f′（0）x＋
！f″（0）x2＋
f‴（η）x3，η介于0与x之间；令x＝－1，x＝1，分别有：
0＝f（－1）＝f（0）＋
，－1＜＜0，η1
1＝f（1）＝f（0）＋
，0＜η2＜1.
三式相减可有：f‴（η1）＋f‴（η2）＝6.
由f‴（x）的连续性，在［η1，η2］上有最大值M与最小值m，则有m≤f‴（η1）≤M，m≤f‴（η2）≤M.
由介值定理有ξ∈［η1，η2］⊂［－1，1］，使
8.连续.
9.f′（x）单调递增，对f（x）在［0，1］利用拉格朗日中值定理，f（1）－f（0）＝f′（ξ）（0＜ξ＜1），故f′（0）＜f′（ξ）＜f′（1）
11.设f（x）＝
（x≥1），x＝e为f（x）的唯一驻点，可判断为最大值点从而比较e附近的x＝2与x＝3的值知
为最大项.
12.拐点A1（－1，－1），A2（2－
13.（1，4），（1，－4）.
14.y＝0为水平渐近线；x＝0，x＝－2均为铅直渐近线；无斜渐近线.
15.x＞a时，f″（x）＞0，从而f′（x）单调递减，则f′（x）＜f′（a）＜0.
由拉格朗日中值定理，对任何x＞a，存在ξ∈（a，x），使
f（x）－f（a）＝f′（ξ）（x－a）＜f′（a）（x－a），
即
f（x）＜f（a）＋f′（a）（x－a）.
又f′（a）＜0，知x充分大时f′（a）（x－a）＜－f（a），从而f（x）＜0，故存在b＞a，使f（b）＜0，则在（a，b）内仅有一实根.
16.证：对F（x）在［0，1］上利用罗尔定理，存在ξ1∈（0，1），使得F′（ξ1）＝0.
又F′（x）＝3x2 f（x）＋x3 f′（x），知F′（0）＝0.
对F′（x）在［0，ξ1］上应用罗尔定理，存在ξ2∈（0，ξ1），使得F″（ξ2）＝0.
而F″（x）＝6xf（x）＋6x2 f′（x）＋x3 f″（x），F″（0）＝0.
故对F″（x）在［0，ξ2］上应用罗尔定理，存在ξ∈（0，ξ2）⊂（0，1），使F‴（ξ）＝0.
17.证：对f（x）在［a，b］上应用拉格朗日中值定理，存在ξ∈（a，b），使f′（ξ）＝
令g（x）＝x2，对f（x），g（x）在［a，b］上应用柯西中值定理得，
存在
即有
从而有
即
18.证：设F（x）＝f（x）－x2.由拉格朗日中值定理，存在η∈（0，1），使得
F′（η）＝F（1）－F（0）＝－1.
又F′（x）＝f′（x）－2x，则F′（1）＝f′（1）－2＝－1＝F′（η）.
对F′（x）在［η，1］上应用罗尔定理，存在ξ∈（η，1）⊂（0，1），使F″（ξ）＝0.
又F″（x）＝f″（x）－2，故f″（ξ）＝2.
19.证：令F（x）＝exf（x），G（x）＝ex.
对F（x），G（x）在［a，b］上分别应用拉格朗日中值定理.存在ξ，η∈（a，b），使
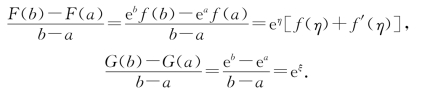
又由条件f（a）＝f（b）＝1，可得eξ＝eη［f（η）＋f′（η）］，
即eη－ξ［f（η）＋f′（η）］＝1.
20.解：设f（x）＝ex－ex－b，有f′（x）＝ex－e.
可求得驻点x＝1，且f（1）＝－b.
当x＞1时，f′（x）＞0；当x＜1时，f′（x）＜0.
因此f（x）在［－∞，1］上严格单调递减；在［1，＋∞）上严格单调递增.
又
f（x）＝
f（x）＝＋∞，f（1）＝－b.
故b＝0时，f（1）＝0.原方程有唯一实根x＝1；
故b＜0时，f（1）＞0.原方程无实根；
故b＞0时，f（1）＜0.原方程分别在（－∞，1）及（1，＋∞）上各存在一个实根，共有两个实根.