习题6－6

习题6－6

1.（1）相关； （2）无关； （3）无关； （4）无关； （5）无关； （6）无关.

2.y＝C1x＋C2ex＋x2.

3.y＝C1e2x＋C2e－x＋

6.y＝C1ex＋C2（2x＋1）.

7.y＝C1ex＋C2e2x.

8.证：因y1（x），y2（x）是方程的解，故有

y″1＋p（x）y′1＋q（x）y1＝0，y″2＋p（x）y′2＋q（x）y2＝0.

两式分别乘以y2，y1，再相减得

y″1·y2－y″2·y1－p（x）（y1y′2－y′1y2）＝0.

若令A（x）＝y1y′2－y′1y2，则易得A′（x）＝y1y″2－y″1y2，

故上述方程可变为

A′（x）＋p（x）A（x）＝0.

从而有A（x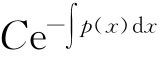）＝，原结论成立.

9.（3）此为线性微分方程，并可变为

这里p（x）＝－，q（x）＝，满足1＋p（x）＋q（x）＝0且p（x）＋xq（x）＝0.

故方程有解y1＝ex和y2＝x，从而方程通解为y＝C1ex＋C2x.

代入有

y（0）＝C1e0＝2⇒C1＝2，

y′＝C1ex＋C2， y′（0）＝1，

⇒2＋C2＝1⇒C2＝－1.

于是特解为y＝2ex－x.