型不定式的极限

二、 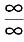型不定式的极限

定理2 若函数f（x）与g（x）满足：

（1）

（2）在x0的某右邻域内二者均可导，且g′（x）≠0；

（3）＝A（A可为实数，也可为±∞或∞）；

则

证 先设A为实数，由条件（3），对任给正数ε，存在x1∈U＋（x0），使得对任何x∈（x0，x1），有

再由条件（2），将f（x）与g（x）在［x，x1］上利用柯西中值定理，则存在ξ∈（x，x1）⊂（x0，x1），使得

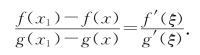
由上面所证式（1），有

又

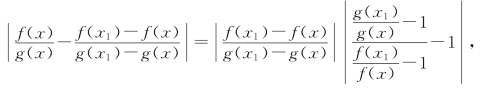
由式（2）可知，右边第一个因子为有界量；由于f（x），g（x）均为无穷大量，对于固定的x1，右边第二个因子在x→x0时是无穷小量.因而存在正数δ，使得x∈（x0，x0＋δ）⊂（x0，x1）时有

从而对一切x∈（x0，x0＋δ），由式（2）和式（3），有

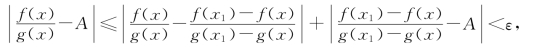
这就证明

类似可证明A＝±∞或∞的情形，这里不再赘述.

定理对于x→，x→x0，x→±∞，x→∞等情形也有同样的结论.

例6 求极限（α＞0）.

解 这是型不定式极限.利用洛必达法则有

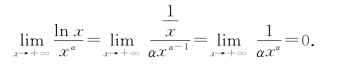
例7 求极限（，）α＞0a＞1.

解 这是型不定式极限，利用洛必达法则有

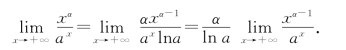
上式分子次数降低一次，若α－1≤0，右端极限为0.

若α－1＞0，连续用洛必达法则直至分子次数不大于0，即

由以上两例可知，在x→＋∞时，ax（a＞1）是较xα（α＞0）高阶的无穷大量，而xα（α＞0）是较ln x高阶的无穷大量.以后在涉及无穷大量阶的比较时可直接利用上述结论.

还需指出的是，定理中的条件只是充分条件.若不存在，并不意味着也不存在，只是此时用洛必达法则失效，需寻求其他方法计算.

例如，极限是型，利用洛必达法则计算有

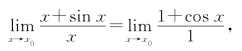
右端极限不存在，并不能说明原式极限也不存在.

用以下方法可求此极限：