函数的可导性与连续性
类似于函数在一点处的左极限和右极限，下面定义是函数在一点处的左导数和右导数.
定义2 若极限
存在，则称此极限值为函数y＝f（x）在点x0处的左导数，记作f′－（x0）.
同理，函数y＝f（x）在点x0处的右导数为
显然，函数f（x）在点x0处可导的充分必要条件是：f′－（x0）＝f′＋（x0）＝f′（x0）.
如果函数f（x）在开区间（a，b）内可导，并且在x＝a的右导数存在，在x＝b的左导数存在，则称f（x）在闭区间［a，b］上可导.
例6 讨论函数y＝
在x＝0点的可导性.
解 函数在x＝0附近有定义，且在x＝0连续，即
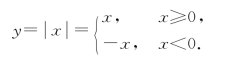
考虑它在x＝0的左导数和右导数，有
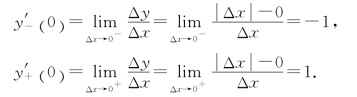
函数在x＝0的左、右导数都存在，但不相等，故y＝
在x＝0点不可导.但当x≠0时，函数y＝
可导，且（
）′＝
定理1 若函数y＝f（x）在点x0处可导，则y＝f（x）在点x0处连续.
证 设自变量在x0点处的改变量为Δx，相应的函数的改变量为Δy，又因为函数在点x0可导，所以
即
所以函数y＝f（x）在点x0连续.
例7 讨论函数f（x）＝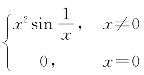
在点x＝0的连续性与可导性.
解 因为
＝0＝f（0），所以函数f（x）在x＝0连续.
由导数的定义得
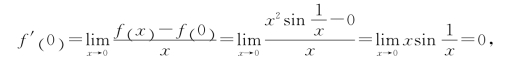
所以f（x）在x＝0可导，且f′（0）＝0.
例8 讨论函数f（x）＝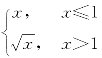
在点x＝1的连续性与可导性.
解 函数f（x）在x＝1处的左、右两侧表达式不同，要分别求其左、右极限和左、右导数.
因为
即
所以函数f（x）在x＝1连续.
又
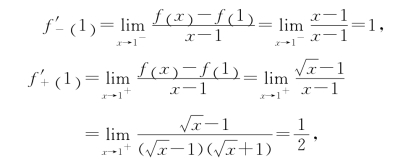
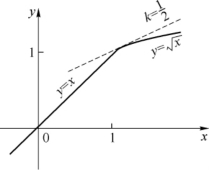
图2－2
在x＝1处左、右导数存在但不相等（见图2－2），所以函数f（x）在x＝1处不可导.
若函数在一点P可导，从函数图形上看，在该点处应该是“光滑”的，没有“尖点”.例如y＝｜x｜，在x＝0处其函数图形具有“尖点”（见图1－4），所以在x＝0点不可导.
由以上各例可知，“连续”是函数“可导”的必要条件，而非充分条件.即函数在一点处不连续，则在该点必不可导.