可化为一阶线性微分方程的类型

二、可化为一阶线性微分方程的类型

（1）伯努利（Bernoulli）方程

型如

的方程称为伯努利方程.特别地，当n＝0或n＝1时，上述方程是一阶线性微分方程.下面讨论其解法.

将方程（10）两边同时除以yn，得

即

若令z＝y1－n，则

是z关于x的一阶线性方程，求出通解后，以y1－n代替z即可得伯努利方程的通解.

例3 解方程

解 原方程可化为，是伯努利方程.两端同时除以y－1，得

凑微分，得

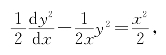
令z＝y2则化为

这是一阶线性方程.可求其通解为

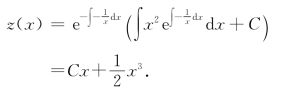
把z＝y2代入，得原方程通解为

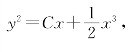
其中C为任意常数.

（2）其他可化为一阶线性微分方程的例子

例4 解方程（1＋y2）dx＋（x－arctan y）dy＝0.

解 原方程可化为.此为以x为因变量，y为自变量的一阶线性微分方程.

由（6）式可得通解为

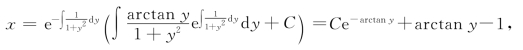
其中C为任意常数.

例5 解方程xy′（ln x）sin y＋cos y（1－xcos y）＝0.

解 原方程既不是线性方程，也不是伯努利方程，但可将原方程变形为

令cos y＝z，则方程（12）化为

是伯努利方程.令u＝z－1，则方程（13）化为

由（6）式得方程（14）的通解为

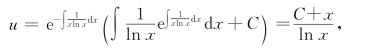
其中C为任意常数.

将u＝z－1及z＝cos y代入上式，得原方程通解为

（x＋C）cos y＝ln x.

还有一种常见可解的一阶微分方程为全微分方程，有关此类方程解法放到多元微分学后介绍.