一、定积分的概念
实际的应用中经常要计算这样一些量.例如，几何上，求一个不规则的平面图形的面积，求一个不规则的几何体的体积；物理上，求质点在连续变化的外力作用下沿直线或曲线移动所做的功，求密度不均匀的物体的质量等.如何精确计算这些量呢？需利用极限这一工具.在初等数学中圆面积就是用边数无限增多的内接正多边形的面积的极限来定义的.现在仍用极限的思想定义这些量，从而引入定积分的概念.先看以下两例.
1.曲边梯形的面积
设f（x）≥0为闭区间［a，b］上的连续函数，由曲线y＝f（x），直线x＝a，x＝b及x轴围成的平面图形（见图5－1）称为曲边梯形.
下面用极限这一工具定义曲边梯形的面积.需先求近似值.设想在图5－1中，f（x）的定义域［a，b］内取一个很小的闭区间［α，β］，则连续函数f（x）的值在其上的变化不大.从而小区间［α，β］对应的小曲边梯形的面积可近似用矩形面积代替.基于这种思想，则在闭区间内任取n－1个分点（n很大），依次为
a＝x0＜x1＜x2＜…＜xn－1＜xn＝b，
这样，［a，b］被分割为n个小区间［xi－1，xi］（i＝1，2，…，n）.画出所有直线x＝xi（i＝1，2，…，n），因此曲边梯形就被分割为n个小曲边梯形（见图5－2）.
在第i个小区间［xi－1，xi］上任取一点ξi，作以f（ξi）为高，［xi－1，xi］为底的小矩形，i＝1，2，…，n.由于每个小区间［xi－1，xi］很小，从而用小矩形的面积近似代替小曲边梯形的面积.这样小矩形的面积和
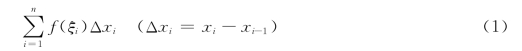
就是曲边梯形面积的近似值.若当分点无限增多，分割无限加细时，和式（1）无限接近某一常数，就把此常数定义为曲边梯形的面积.
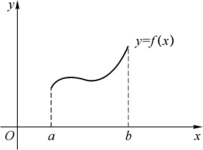
图5－1
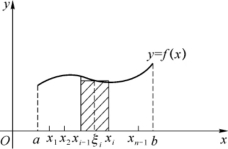
图5－2
2.变力沿直线做功
如图5－3所示，设质点在平行于x轴的力F（x）的作用下从a点移动到b点，下面定义变力F（x）所做的功.如果F（x）为常力，很容易计算出所做的功.现在设F（x）是连续依赖于质点所在位置x变化的变力，即F（x）为连续函数，则仍需先求近似值.
图5－3
类似于曲边梯形面积的求法，将［a，b］分成n个小区间［xi－1，xi］，i＝1，2，…，n.在第i个小区间上任取一点ξi，用F（ξi）近似代替区间［xi－1，xi］上各点所受的力.因此，质点从xi－1移动到xi所做的功近似为F（ξi）Δxi（Δxi＝xi－xi－1）.这样，质点在F（x）的作用下从点a移动到点b所做的功的近似值为
同样，若当分点无限增多，分割无限加细时，和式（2）无限接近某个常数，就把此常数定义为变力F（x）所做的功.
上面两例，一个是几何问题，一个是物理问题，尽管表面上看毫不相关，但却有一个同样的要求：计算一个和式的极限.因此有必要将类似的问题经过数学抽象使它们统一建立在严格的理论基础上，这就产生了定积分的概念，其思想方法概括起来就是“分割、近似求和、取限”.
定义1 设函数f（x）在区间［a，b］上有定义，在区间［a，b］内任取n－1个分点
a＝x0＜x1＜x2＜…＜xn－1＜xn＝b，
将区间分割为n－1个小区间［xi－1，xi］（i＝1，2，…，n），长度记为Δxi＝xi－xi－1（i＝1，2，…，n）.在每个小区间［xi－1，xi］上任取一点ξi，作和式
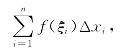
令λ＝max｛Δx1，Δx2，…，Δxn｝.若当λ→0时，和式的极限存在，且此极限值不依赖于对区间［a，b］的分割，也不依赖于｛ξi｝（i＝1，2，…，n）的取法，称函数f（x）在区间［a，b］上黎曼可积或可积，称此极限值为函数f（x）在区间［a，b］上的黎曼积分或定积分，记为
f（x）dx，即
其中，f（x）称为被积函数，f（x）dx称为被积表达式，x称为积分变量，a和b分别称为积分下限与积分上限，［a，b］称为积分区间.并称和式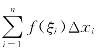
为函数f（x）在区间［a，b］上的一个积分和或黎曼和.
注意 对定义中的分割，称λ为这个分割的分割细度，称点集｛ξi：1≤2≤n｝为属于这个分割的一个介点集.比较积分和的极限与一般函数的极限
不难发现二者区别很大：对函数的极限而言，自变量x在趋于a的过程中，每个x对应的函数值能唯一确定；对积分和的极限而言，在分割细度趋于0的变化过程中，积分和并非由λ唯一确定.这是由于同一分割细度可对应无穷多种分割，而每一种分割，又会有无穷多个介点集，从而使每一个分割细度λ对应无穷多个积分和.因此，通过直接计算所有积分和再取极限去求一个函数的定积分是无法实现的.但是，在已知定积分存在（可积）的前提下，可选择特殊的分割和特殊的介点集，将此时构成的积分和化为数列，可以通过求数列的极限求得定积分.
由于闭区间上定义的连续函数可积（稍后给出此结论），从而可以计算以下定积分.
例1 求由曲线y＝x2，直线x＝0，x＝1及x轴围成的曲边梯形的面积S.
解 由于y＝x2，在［0，1］上连续，从而可积，则可选取特殊分割和特殊介点集构造积分和来求定积分
，即求得曲边梯形的面积S（见图5－4）.
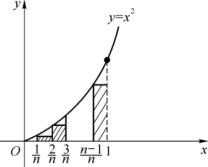
图5－4
为此，等分区间［0，1］为n份，分点为
分割细度λ＝
.取介点集为每个小区间[
］的左端点，即ξi＝
（i＝1，2，…，n）.则对应的积分和为
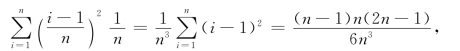
又分割细度λ→0时，有n→∞.那么所求的曲边梯形的面积为
注意 定积分为积分和的极限，它的值只由被积函数和积分区间决定，与积分变量选用的符号无关，即
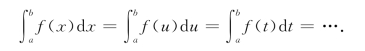
对于闭区间［a，b］上的连续函数f（x），结合对应的曲边梯形，定积分
有这样的几何意义：
（1）若f（x）≥0，它表示位于x轴上方的曲边梯形的面积；
（2）若f（x）≤0，由定积分的定义可知它表示位于x轴下方的曲边梯形的面积的相反数，称之为“负面积”；
（3）若f（x）既取正值又取负值时，它表示位于x轴上方的所有曲边梯形的正面积与位于x轴下方所有曲边梯形的负面积的代数和，如图5－5所示.
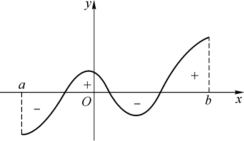
图5－5
此外，若f（x）≥0，在物理上，定积分还可表示质点受变力f（x）作用沿直线由a运动到b所做的功，或可表示物体以变速度f（x）沿直线由a行驶到b所走的路程等.
定积分定义中的区间为有限闭区间［a，b］（a＜b），因此积分下限小于积分上限.为了方便应用作两点补充规定：
（1）
（2）
由定积分与几何意义和物理意义不难理解它们的合理性.