习题3－1
1.（1）证明方程x3－3x＋C＝0（C为常数）在区间［0，1］内不可能有两个不同的实根；
（2）证明方程xn＋px＋q＝0（n为正整数，p、q为实数）当n为偶数时至多有两个实根，当n为奇数时至多有三个实根.
2.不用求出函数f（x）＝（x－1）（x－2）（x－3）（x－4）的导数，说明方程f′（x）＝0至少有几个实根，并指出它们所在的区间.
3.若方程a0xn＋a1xn－1＋…＋an－1x＝0有一正根x0，证明方程a0nxn－1＋a1（n－1）xn－2＋…＋an－1＝0必有一个小于x0的正根.
4.f（x）在［a，b］上有二阶导数，且f（a）＝f（b）＝0，又F（x）＝（x－a）f（x）.证明在（a，b）内至少存在一点ξ，使F″（ξ）＝0.
5.设g（x）在闭区间［a，b］上连续，且在（a，b）内可导，又设对（a，b）内所有x，g′（x）≠0，则在（a，b）内至少有一点ξ，使
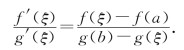
6.证明下列不等式：
（1）
，其中0＜a＜b； （2）
＜arctan h＜h，其中h＞0.
7.证明不等式：
（1）｜arctan a－arctan b｜≤｜a－b｜；（2）当x＞1时，ex＞ex.
8.设函数f（x）在［a，b］上二阶可导，f（a）＝f（b）＝0，且存在一点c∈（a，b），使f（c）＞0，证明至少存在一点ξ∈（a，b），使f″（ξ）＜0.
9.设f（x）在［a，b］上连续，在（a，b）内二阶可导.连接点（a，f（a））和（b，f（b））的直线与曲线y＝f（x）交于点（c1，f（c））及（c2，f（c2））（a＜c1＜c2＜b）.证明在（a，b）内至少存在两点ξ1与ξ2，使f″（ξ1）＝f″（ξ2）＝0.
10.设f（x）在［a，b］上连续，在（a，b）内可导，且ab＞0，证明在（a，b）内至少存在一点ξ，使
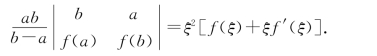
11.设x1，x2＞0，证明在x1与x2之间存在ξ，使
12.设f（x）在［a，b］（0＜a＜b）上连续，在（a，b）内可导.证明在（a，b）内存在ξ，η，使得
