函数的初等性态
1.奇偶性
设y＝f（x）的定义域D关于原点对称.如果
f （－x）＝f（x）， ∀x∈D，
则称f（x）为偶函数，函数图像关于y轴对称；如果
f （－x）＝－f（x）， ∀x∈D，
则称f（x）为奇函数，函数图像关于坐标原点中心对称.
例如，定义域为（－∞，＋∞）的函数f（x）＝sin x是奇函数，g（x）＝cos x是偶函数，而函数h （x）＝sin x＋cos x既非奇函数又非偶函数.
2.周期性
设函数f（x）在D＝（－∞，＋∞）上有定义，若∃T＞0，使得对∀x∈D有
f （x＋T）＝f（x）
成立，则称f（x）是以T为周期的周期函数.满足上述关系的最小正数T称为函数f（x）的最小正周期.通常说的周期指最小正周期（如果存在）.
例如，函数f（x）＝sin x，g（x）＝cos x都是周期函数，2π、4π等都是它们的周期，2π是其最小正周期.
3.单调性
设f（x）的定义域为D，区间I⊂D，如果∀x1，x2∈I，当x1＜x2时，总有
f （x1）≤f （x2） （或f （x1）≥f （x2））
成立，则称函数f（x）在区间I上单调递增（或单调递减）；如果等号不成立，则称函数f（x）在区间I上严格单调递增（或严格单调递减），如图1－7所示.单调递增的函数和单调递减的函数统称为单调函数.
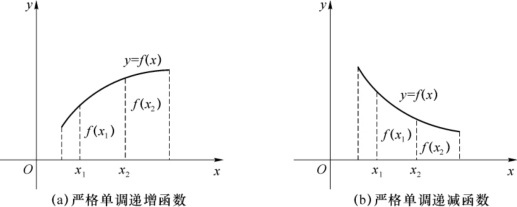
图1－7
例如，ff（x）＝［x］在（－∞，＋∞）上单调递增，但不是严格单调递增；y＝x2在（－∞，0］上严格单调递减，在［0，＋∞）上严格单调递增.此时，称f（x）在（－∞，＋∞）上分段单调.
4.有界性
设f（x）的定义域为D，数集A⊂D.如果∃M＞0（M为常数），使得对∀x∈A，
总成立，则称f（x）在A上有界，或称f（x）是A上的有界函数.若对∀M＞0，总∃x0∈A⊂D，使得
＞M，则称f（x）在A上无界.
例如，y＝sin x在（－∞，＋∞）上有界，因为存在常数M＝1，使得对∀x∈（－∞，＋∞）都有
≤1.
对某个函数f（x），定义域为D，可能出现下面情况：它在子集A⊂D上有界，而在另一子集B⊂D上无界.例如，y＝
在定义域D＝（－∞，0）∪（0，＋∞）上无界，但对∀δ＞0，它在子集（－∞，－δ］和［δ，＋∞）上有界.
设f（x）的定义域为D，A⊂D，如果存在常数M，使得对∀x∈A，都有f（x）≤M，则称f（x）在A上有上界M；若存在常数m，使得对∀x∈A，都有f（x）≥m，则称f（x）在A上有下界m.
函数f（x）在A上既有上界又有下界的充分必要条件是f（x）在A上有界.