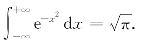无界函数的反常积分
1.无界函数反常积分的概念
定义1 设函数f(x)定义在区间(a,b]上,且在点a的任何右邻域内无界,但在任何闭区间[u,b]⊂(a,b]内有界可积,若存在极限
![]()
则称此极限为无界函数f(x)在(a,b]上的反常积分(或称瑕积分,点a为f(x)的瑕点),记为
![]()
此时,称反常积分![]() f(x)dx收敛;若极限(5)不存在,称反常积分
f(x)dx收敛;若极限(5)不存在,称反常积分![]() f(x)dx发散.
f(x)dx发散.
类似地,可定义b为f(x)的瑕点时的瑕积分
![]()
若f(x)的瑕点为c∈(a,b),且f(x)在[a,c)与(c,b]内任何闭区间上可积时,如果瑕积分
![]()
均收敛,称二者之和为函数f(x)在[a,b]上的反常积分,记为
![]()
此时,也称反常积分![]() f(x)dx收敛;否则若(6)中二者至少有一个发散时,称反常积分
f(x)dx收敛;否则若(6)中二者至少有一个发散时,称反常积分![]() (x)dx发散.
(x)dx发散.
类似地,若f(x)的瑕点为a和b时,可定义反常积分
![]()
例5 计算瑕积分![]()
解 x=1为f(x)=![]() 的瑕点.则有
的瑕点.则有
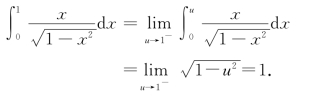
例6 讨论瑕积分
![]()
的敛散性.
解 x=a为被积函数f(x)=![]() 的瑕点,由于
的瑕点,由于
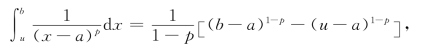
从而
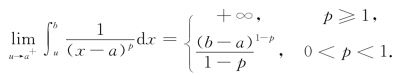
即当0<p<1时,积分收敛;当p≥1时,积分发散.
类似可证明反常积分![]() 在时收敛,在时发散dx0<p<1p≥1.
在时收敛,在时发散dx0<p<1p≥1.
2*.无界函数反常积分敛散性的判别
类似无穷积分敛散性判别,有相应的定理.
定理(柯西准则) 瑕积分![]() f(x)dx(a为瑕点)收敛的充要条件为:任给ε>0,存在δ>0,只要u1,u2∈(a,a+δ),就有
f(x)dx(a为瑕点)收敛的充要条件为:任给ε>0,存在δ>0,只要u1,u2∈(a,a+δ),就有
![]()
定理 若函数f(x)(瑕点为a)在(a,b]的任一闭区间[u,b]⊂(a,b]上可积,则当![]() |f(x)|dx收敛时,
|f(x)|dx收敛时,![]() f(x)dx也收敛,并且
f(x)dx也收敛,并且
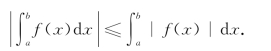
类似无穷积分,当![]() |f(x)|dx收敛时,称
|f(x)|dx收敛时,称![]() f(x)dx绝对收敛;当
f(x)dx绝对收敛;当![]() |f(x)|dx发散,而f(x)dx收敛时,称
|f(x)|dx发散,而f(x)dx收敛时,称![]() f(x)dx条件收敛.
f(x)dx条件收敛.
![]()
定理(比较法则) 设非负函数f(x),g(x)为定义在(a,b]上的两个函数,瑕点均为a,且均在任何[u,b]⊂(a,b]上可积,并满足
f(x)≤g(x), x∈(a,b],
则当![]() g(x)dx收敛时,
g(x)dx收敛时,![]() f(x)dx也收敛(或当
f(x)dx也收敛(或当![]() f(x)dx发散时,
f(x)dx发散时,![]() g(x)dx也发散).
g(x)dx也发散).
推论1(比较法的极限形式) 设非负函数f(x),g(x)均以a为瑕点,且![]() =c,则有:
=c,则有:
(1)当0<c<+∞时,![]() f(x)dx与
f(x)dx与![]() g(x)dx敛散性相同;
g(x)dx敛散性相同;
(2)当c=0时,由![]() g(x)dx收敛可推得
g(x)dx收敛可推得![]() f(x)dx也收敛;
f(x)dx也收敛;
(3)当c=+∞时,由![]() f(x)dx收敛可推得
f(x)dx收敛可推得![]() g(x)dx也收敛.
g(x)dx也收敛.
推论2 设f(x)为(a,b]上的非负函数,以a为其瑕点,且在任何[u,b]⊂(a,b]上可积,则有:
(1)当f(x)≤![]() ,且0<p<1时,
,且0<p<1时,![]() (x)dx收敛;
(x)dx收敛;
(2)当f(x)≥![]() ,且p≥1时,
,且p≥1时,![]() f(x)dx发散.
f(x)dx发散.
推论3 设f(x)为(a,b]上的非负函数,a为其瑕点,且在任何[u,b]⊂(a,b]上可积,如果
![]()
则有:
(1)当0<p<1,0≤λ<+∞时,![]() f(x)dx收敛;
f(x)dx收敛;
(2)当p≥1,0<λ≤+∞时,![]() f(x)dx发散.
f(x)dx发散.
例7 讨论下列瑕积分的敛散性:

解 (1)x=0为被积函数的瑕点.
又![]() =1,此时p=
=1,此时p=![]() ,由推论3知此瑕积分收敛.
,由推论3知此瑕积分收敛.
(2)被积函数只以x=0为瑕点.x=1不为瑕点,因为利用洛必达法则有
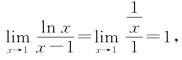
则被积函数在x=1的任何邻域内不为无界函数.
又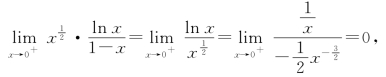
此时p=![]() ,利用推论3知此积分收敛.
,利用推论3知此积分收敛.
例8 讨论反常积分
![]()
的敛散性.
解 当α<1时,x=0为被积函数的瑕点;当β<1时,x=1为被积函数的瑕点.
![]()
①α≥1且β≥1,I与J均为定积分.
②α<1时
![]()
当p<1-α<1,即0<α<1时,I收敛;
当1-α≥1,即α≤0时,I发散.
③β<1时
![]()
当0<1-β<1,即0<β<1时,J收敛;
当1-β≥1,即β≤0时,J发散.
综上,只有α>0且β>0时,I与J均收敛,B(α,β)收敛.
这个函数称为β-函数,今后会发现它有很重要的应用.
例9 讨论反常积分
![]()
的敛散性.
解![]()
当s≥1时,I为定积分,s<1时,I的被积函数以0为瑕点.又
![]()
所以,当0<1-s<1,即0<s<1时,I收敛.
当1-s≥1,即s≤0时,I发散.
![]()
此时p=2,J收敛(无论s为任何值).
综上,只有s>0时,I与J均收敛,从而广义积分收敛.
此函数Γ(s)称为Γ函数,与β函数一样,有着广泛的应用.
利用分部积分法可证明Γ-函数有递推公式
Γ(s+1)=sΓ(s) (s>0),
反复利用递推公式,并注意到Γ(1)=![]() e-xdx=1,则对任何自然数n,有
e-xdx=1,则对任何自然数n,有
Γ(n+1)=n!.
利用余元公式Γ(s)Γ(1-s)=![]() (0<s<1)(证略),
(0<s<1)(证略),
可得Γ(![]() )=
)=![]() ,并将(7)式中x代换为u2,有
,并将(7)式中x代换为u2,有
![]()
再令s=![]() ,得概率中常用的泊松积分
,得概率中常用的泊松积分