总习题五
1.设f（x）在［0，1］上连续，且f（x）＞0，求
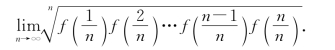
2.计算
sin22x（tan x＋1）dx.
3.f（x）有二阶连续导数，且
［f（x）＋f″（x）］sin xdx＝5，f（π）＝2，求f（0）.
4.设f（x）＝
dt（x＞0），求f（x）＋f（
）.
5.设x≥－1，求
（1－｜t｜）dt.
6.设f（x）在［a，b］上具有二阶连续导数，求证存在ξ∈（a，b），使
7.设f（x）＝
dt，求f′（x）.
8.设f（x）连续，且
f（t）dt＝x.求f（7）.
9.设f（x）＝
）dt，求f″（x）.
10.确定a，b，c的值，使
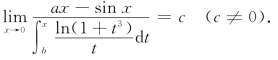
11.设α（x）＝
dt，β（x）＝
dt，则当x→0时，α（x）是β（x）的（ ）.
（A）高阶天穷小 （B）低阶无穷小
（C）同阶不等价无穷小 （D）等价无穷小
12.设f（x）有连续导数，f（0）＝0，f′（0）≠0.F（x）＝
（x2－t）f（t）dt.当x→0时，F（x）与xk同阶无穷小，则k等于（ ）.
（A）1 （B）2 （C）3 （D）4
13.求
dx.
14.设f（x）在［a，b］上连续，且f（x）＞0，x∈［a，b］，
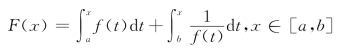
证明：（1）f′（x）≥2；
（2）方程F（x）＝0在区间（a，b）内有且只有一根.
15.设f（x）在［a，b］上二次可导，且f″（x）＞0，证明：
16.试确定常数c的值，使下列反常积分收敛并求值.
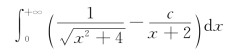
17.已知
＝1，求a，b的值.
18.计算广义积分
（ln x）ndx，n∈N＋.
19.求曲线y＝
的一条切线L，使该曲线与切线L及直线x＝0，x＝2所围成的平面图形面积最小.
20.设有抛物线T：y＝a－bx2（a＞0，b＞0），试确定常数a，b的值，使得：
（1）T与直线y＝x＋1相切；
（2）T与x轴所围图形绕y轴旋转而成的旋转体的体积最大.
21.求曲线y＝
的弧长.
22.填空题.
（1）f（x）是连续函数，
tf（ x2－t2）dt＝
（2）f（x）二阶连续可微，f（2）＝
，f′（2）＝0，
f（x）dx＝1，则
x2 f″（2x）dx＝
（3）f（x）连续，且f（x）＝x＋2
f（t）dt，则f（x）＝
（4）f（x）＝
dy，则
（5）f（x）＝
dy，则
（x－1）2 f（x）dx＝
（6）
［f（x）f（－x）］＋tan xdx＝
23.判断广义积分
dx的敛散性.
24.设f（x）＝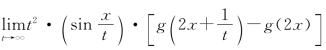
，其中g（x）可导，且g（x）的一个原函数为ln（x＋1），计算积分
f（x）dx.
25.设f（x）是一个连续函数，φ（x）＝
f（xt）dt，且
＝A（A为常数），求φ′（x），并讨论φ′（x）在x＝0处的连续性.
26.设函数f（x）在（－L，L）内连续，在x＝0可导，f′（0）≠0.
（1）证明：对任意给定的x∈（0，L），存在θ∈（0，1），使得
f（t）dt＋
f（t）dt＝x［f（θx）－f（－θx）］.
（2）求极限