拉格朗日中值定理与柯西中值定理
将罗尔定理中的条件(3)去掉,考虑更一般的情形,便得到微分学中非常重要的拉格朗日中值定理.
拉格朗日中值定理 如果函数f(x)满足如下条件:
(1)在闭区间[a,b]上连续;
(2)在开区间(a,b)内可导;则在(a,b)内至少存在一点ξ,使得
![]()
拉格朗日中值定理的几何意义是:在处处可导的一段曲线上,至少存在一点,使该点处的切线平行于曲线两端点的连线(见图3-5).
证 作辅助函数
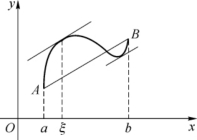
图3-5
![]()
显然,F(a)=F(b)=0,在[a,b]上对F(x)利用罗尔定理,存在ξ∈(a,b),使
![]()
即
![]()
若在此定理条件中加入f(a)=f(b),便得到罗尔定理.因此罗尔定理是此定理的特殊情形.
拉格朗日中值定理中的式(1)称为拉格朗日中值公式.拉格朗日中值公式还有以下几种等价形式,供读者在不同场合下选用:
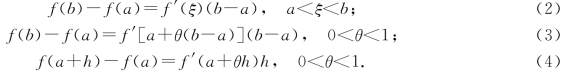
值得注意的是,拉格朗日中值式(1)~式(4),不论a>b还是a<b都成立.式(1)、式(2)中的中值ξ是介于a与b之间某一定数.式(3)、式(4)中把中值ξ表示成了a+θ(b-a)或a+θh,不论a与b为何值,θ总为小于1的某一正数.
例3 设f(x)在[a,b]上连续,在(a,b)内可导.证明至少存在一点ξ∈(a,b),使
![]()
证 设F(x)=xf(x).
利用连续函数及可导函数的乘积的性质可知,F(x)在[a,b]上满足拉格朗日中值定理的条件.从而至少存在一点ξ∈(a,b),使
![]()
即
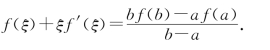
例4 证明不等式![]() <ln(1+h)<h,(h>-1,h≠0).
<ln(1+h)<h,(h>-1,h≠0).
证 设F(x)=ln(1+x).
分以下两种情况:
(1)h>0,此时F(x)在[0,h]上满足拉格朗日中值定理的条件,从而存在ξ∈(0,h),使
![]()
即
![]()
注意到0<ξ<h,有
![]()
则
![]()
于是
![]()
(2)-1<h<0,此时F(x)在[h,0]上满足拉格朗日中值定理的条件,从而存在ξ∈(h,0),使
![]()
即
![]()
注意到-1<h<ξ<0,有
![]()
则
![]()
于是
![]()
例5 设f(x)在区间I上可导,且导函数有界.证明f(x)在区间I上满足李普希兹条件(存在正数M,使得对任何,x1,x2∈I,有|f(x1)-f(x2)|≤M|x1-x2|).
证 由于f′(x)在I上有界,则存在函数M,使
|f′(x)|≤M (x∈I).
任取x1,x2∈I.在区间[x1,x2](或[x2,x1])上利用拉格朗日中值定理,存在介于x1与x2之间的ξ,使
f(x1)-f(x2)=f′(ξ)(x1-x2),
从而有
|f(x1)-f(x2)|=|f′(ξ)||x1-x2|≤M|x1-x2|.
推论1 若函数f(x)在区间I上可导,且f′(x)=0,则f(x)在区间I上为常数.
证 任取x1,x2∈I,不妨设x1<x2.
在[x1,x2]上利用拉格朗日中值定理,则存在ξ∈(x1,x2).使
f(x1)-f(x2)=f′(ξ)(x1-x2)=0,
即
f(x1)=f(x2),
从而知f(x)在I上为常数.
推论2 若函数f(x),g(x)在区间I上均可导,且f′(x)=g′(x),则f(x)与g(x)相差一个常数.
证 设F(x)=f(x)-g(x) (x∈I).
由已知条件知F′(x)=f′(x)-g′(x)=0,利用推论1,F(x)为常数,即f(x)与g(x)相差一个常数.
柯西中值定理 设函数f(x)和g(x)满足如下条件:
(1)在[a,b]上均连续;
(2)在开区间(a,b)内均可导;
(3)对任何x∈(a,b),g′(x)≠0,则在(a,b)内至少存在一点ξ,使得
![]()
证 作辅助函数F(x),有
![]()
(定理条件保证分母g(b)-g(a)≠0,为什么?)
易知F(x)在[a,b]上满足罗尔定理条件,故存在ξ∈(a,b),使得
![]()
由于g′(ξ)≠0,所以有
![]()
很明显,若取g(x)=x,式(5)即为拉格朗日中值公式.
柯西中值定理与拉格朗日中值定理有同样的几何意义,只需把曲线视为以x为参量的参量方程
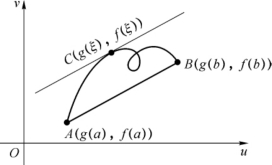
图3-6
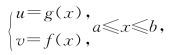
在uov平面上表示的一段曲线(见图3-6).式(5)左端表示连接曲线两端点的线段AB的斜率,右端表示曲线上与x=ξ相对应的一点C(g(ξ),f(ξ))处的切线的斜率,v对u按参数方程求导法则求得的导数
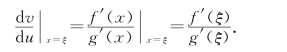
因此,式(1)表示弦AB与此切线平行.
例6 设函数f(x)在[a,b](a>0)上连续,在(a,b)内可导,则存在ξ∈(a,b),使得
![]()
证 设g(x)=ln x,它与f(x)在[a,b]上一起满足柯西中值定理条件,于是存在ξ∈(a,b),使得
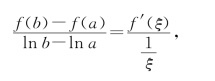
整理后便得f(b)-f(a)=ξf′(ξ)ln![]()
例7 设函数f(x)在a的某邻域内二阶可导,证明对充分小的h,存在θ(0<θ<1),使得
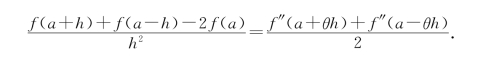
证 若h>0,设F(x)=f(a+x)+f(a-x),G(x)=x2将F(x)、G(x)在[0,h]上利用柯西中值定理,存在ξ1∈(0,h),使
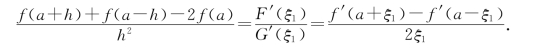
再设F1(x)=f′(a+x)-f′(a-x),G1(x)=x,将F1(x)、G1(x)在[0,ξ1]上利用拉格朗日中值定理,存在ξ∈(0,ξ1)⊂(0,h),使得
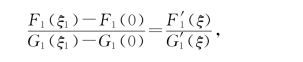
即
![]()
由于ξ∈(0,h),则存在θ(0<θ<1),使ξ=θh.
综合以上结论,便得到
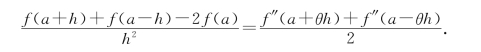
对于h<0的情况可类似讨论.
